设 $\omega$ 为正实数，若存在 $a,b$（$\mathrm{\pi}\leqslant a<b\leqslant 2\mathrm{\pi}$），使得 $\sin\omega a+\sin\omega b=2$，则 $\omega$ 的取值范围是 ．
【难度】
【出处】
2015年全国高中数学联赛（一试）
【标注】
【答案】
$\left[\dfrac 94,\dfrac 52\right]\cup\left[\dfrac {13}{4},+\infty\right)$
【解析】
由 $\sin x\in[-1,1]$ 知，本题条件可以转化成存在 $a,b\in[\mathrm{\pi},2\mathrm{\pi}]$，$a\ne b$，使得$$\sin\omega a=\sin\omega b=1.$$也即 $y=\sin \omega x$ 在 $[\mathrm{\pi},2\mathrm{\pi}]$ 上存在两个不同的最大值点．
$y=\sin\omega x$ 的曲线由正弦曲线 $y=\sin x$ 在横方向上进行伸缩得到的，且必有 $\omega>1$，即图象一定会进行压缩，如图：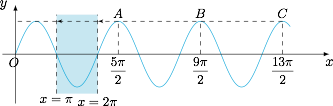
当最大值点 $A,B,C,\cdots$ 中至少存在两个点经过压缩进入阴影区域时，满足题意．
考虑最大值点 $A,B,C,\cdots$ 恰好压缩到边界 $\mathrm{\pi}$ 与 $2\mathrm{\pi}$ 时 $\omega$ 的值，如下：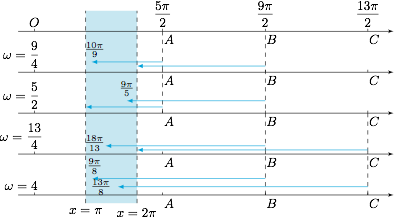
易知当 $\omega$ 从 $1$ 逐渐增大时，$A$ 点先到达右边界 $2\mathrm{\pi}$，此时不满足条件，当 $B$ 点到达右边界时开始满足，直到 $A$ 点到达左边界 $\mathrm{\pi}$，故 $\omega\in\left[\dfrac 94,\dfrac 52\right]$ 时，满足题意；
之后，$\omega$ 继续增加时，$A$ 出左边界，只有 $B$ 点在区域内，此时不满足，直到 $\omega=\dfrac{13}{4}$ 时，$C$ 点压缩到右边界，此时 $B,C$ 两个最值点都在区域内，重新满足条件，直到 $B$ 出左边界，此时需要考虑 $C$ 右边下一个最大值点．
但因为此时 $\omega=\dfrac {9}{2}>4$，边界内已经存在至少两个周期，故此时区域内至少含有两个最大值点，一定满足条件，故 $\omega\geqslant \dfrac {13}{4}$ 时一定满足．
$y=\sin\omega x$ 的曲线由正弦曲线 $y=\sin x$ 在横方向上进行伸缩得到的，且必有 $\omega>1$，即图象一定会进行压缩，如图：
当最大值点 $A,B,C,\cdots$ 中至少存在两个点经过压缩进入阴影区域时，满足题意．考虑最大值点 $A,B,C,\cdots$ 恰好压缩到边界 $\mathrm{\pi}$ 与 $2\mathrm{\pi}$ 时 $\omega$ 的值，如下：
易知当 $\omega$ 从 $1$ 逐渐增大时，$A$ 点先到达右边界 $2\mathrm{\pi}$，此时不满足条件，当 $B$ 点到达右边界时开始满足，直到 $A$ 点到达左边界 $\mathrm{\pi}$，故 $\omega\in\left[\dfrac 94,\dfrac 52\right]$ 时，满足题意；之后，$\omega$ 继续增加时，$A$ 出左边界，只有 $B$ 点在区域内，此时不满足，直到 $\omega=\dfrac{13}{4}$ 时，$C$ 点压缩到右边界，此时 $B,C$ 两个最值点都在区域内，重新满足条件，直到 $B$ 出左边界，此时需要考虑 $C$ 右边下一个最大值点．
但因为此时 $\omega=\dfrac {9}{2}>4$，边界内已经存在至少两个周期，故此时区域内至少含有两个最大值点，一定满足条件，故 $\omega\geqslant \dfrac {13}{4}$ 时一定满足．
题目
答案
解析
备注
