设 $\triangle ABC$，$P_0$ 是边 $AB$ 上一定点，满足 $P_0B=\dfrac 14AB$，且对于边 $AB$ 上任一点 $P$，恒有 $\overrightarrow{PB}\cdot\overrightarrow{PC}\geqslant \overrightarrow{P_0B}\cdot\overrightarrow{P_0C}$，则 $\triangle ABC$ 的形状为 ．
【难度】
【出处】
无
【标注】
【答案】
等腰三角形
【解析】
本题的条件可以翻译为：点 $P$ 在边 $AB$ 上运动，当 $P=P_0$ 时，$\overrightarrow{PB}\cdot\overrightarrow{PC}$ 有最小值．
由极化恒等式知，取 $BC$ 的中点 $M$，有$$\overrightarrow {PB}\cdot\overrightarrow {PC}=PM^2-\dfrac 14BC^2,$$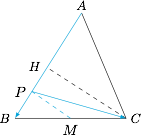
从而知当 $P=P_0$ 时，$PM$ 的长有最小值，即 $P_0M\perp AB$，取 $AB$ 的中点 $H$，有 $P_0M\parallel CH$，所以 $CH\perp AB$，得到 $AC=BC$．
由极化恒等式知，取 $BC$ 的中点 $M$，有$$\overrightarrow {PB}\cdot\overrightarrow {PC}=PM^2-\dfrac 14BC^2,$$
从而知当 $P=P_0$ 时，$PM$ 的长有最小值，即 $P_0M\perp AB$，取 $AB$ 的中点 $H$，有 $P_0M\parallel CH$，所以 $CH\perp AB$，得到 $AC=BC$．
题目
答案
解析
备注
