不妨设 $m>n$，于是 $P(t)$ 即$$\forall m,n\in \mathbb N^*\land m>n,a_m-a_n\geqslant tm-tn,$$即$$\forall m,n\in\mathbb N^*\land m>n,a_m-tm\geqslant a_n-tn,$$即 $\{a_n-tn\}$ 是不减的数列．而数列 $\{a_n-tn\}$ 的差分$$\Delta\left(a_n-tn\right)=\Delta a_n-t,$$其中 $n\in\mathbb N^*\land n\geqslant 2$．因此性质 $P(t)$ 即数列 $\{a_n\}$ 的差分 $\{\Delta a_n\}$ 有下界 $t$．
第一空考虑数列 $\{a_n\}$ 的差分$$\Delta a_n=2^n-2^{n-1}=2^{n-1},$$其中 $n\in\mathbb N^*\land n\geqslant 2$，其最小值为 $2$，因此 $t$ 的最大值为 $2$．
第二空数列 $\{a_n\}$ 的差分$$\Delta a_n=n^2-\dfrac an-\left[(n-1)^2-\dfrac{a}{n-1}\right]=2n-1+\dfrac{a}{n(n-1)},$$根据题意，有$$\forall n\in\mathbb N^*\land n\geqslant 2,2n-1+\dfrac{a}{n(n-1)}\geqslant 10,$$即$$\forall n\in\mathbb N^*\land n\geqslant 2,a\geqslant n(n-1)(11-2n).$$如图，可以根据零点 $n=0,1,\dfrac{11}2$ 勾勒数列 $b_n=n(n-1)(11-2n)$ 的散点图形成的折线形状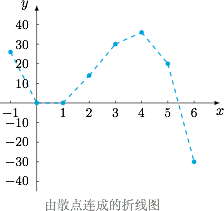．因此右侧的最大值为$$\max\{b_2,b_3,b_4,b_5\}=\max\{14,30,36,20\}=36,$$于是 $a$ 的取值范围是 $[36,+\infty)$．