已知 $f(x)=\dfrac{3+x}{1+x^2}$，$x\in [0,3]$，已知数列 $\{a_n\}$ 满足 $0<a_n\leqslant 3$，$n\in \mathbb N^*$，且$$a_1+a_2+\cdots+a_{2010}=670,$$则$$f\left(a_1\right)+f\left(a_2\right)+\cdots+f\left(a_{2010}\right)$$的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$6030$
【解析】
构造 $x\in [0,3]$ 上的函数不等式$$\dfrac{3+x}{1+x^2}\leqslant -\dfrac{9}{10}\cdot \left(x-\dfrac 13\right)+3.$$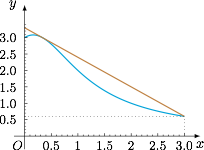
于是有$$\sum_{i=1}^{2010}f(a_i)\leqslant -\dfrac 9{10}\sum_{i=1}^{2010}a_i+\dfrac 3{10}\cdot 2010+3\cdot 2010=6030.$$
于是有$$\sum_{i=1}^{2010}f(a_i)\leqslant -\dfrac 9{10}\sum_{i=1}^{2010}a_i+\dfrac 3{10}\cdot 2010+3\cdot 2010=6030.$$
题目
答案
解析
备注
