记题中关于 $x$ 的不等式左侧为 $g(x,a)$．由于 $g(x,a)\geqslant 0$ 在区间 $\left(0,+\infty\right)$ 上恒成立，分析两个端点 $x\to 0$ 和 $x\to +\infty$，应有必要条件$$\lim_{x\to 0}g(x,a)\geqslant 0\land \lim_{x\to +\infty}g(x,a)\geqslant 0,$$于是不难得到$$a-1\geqslant 0,$$即 $a\geqslant 1$．不难验证 $a=1$ 不符合题意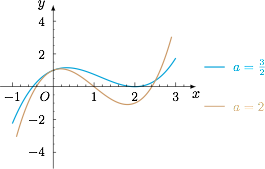．当 $a>1$ 时，注意到 $x^2-ax-1=0$ 的两个实根一正一负，而 $(a-1)x-1=0$ 有一正根 $\dfrac{1}{a-1}$，于是不难推知，这两个方程的正根重合（否则 $g(x,a)$ 在这两个正根之间的取值为负值），因此有$$\left(\dfrac{1}{a-1}\right)^2-a\cdot\dfrac{1}{a-1}-1=0,$$解得$$a=0\lor a=\dfrac 32.$$结合讨论前提，有 $a=\dfrac 32$．接下来 $a=\dfrac 32$ 的充分性容易验证，于是 $a$ 的取值为 $\dfrac 32$．