变量 $x,y$ 满足约束条件 $\begin{cases} y\geqslant -1,\\x-y\geqslant 2,\\3x+y\leqslant 14,\end{cases}$ 若使 $z=ax+y$ 取得最大值的最优解有无穷多个,则实数 $a$ 的取值集合是 .
【难度】
【出处】
无
【标注】
【答案】
$\{-1,3\}$
【解析】
作出可行域,目标函数 $z=(x,y)\cdot(a,1)$,考虑向量 $(x,y)$ 在向量 $(a,1)$ 上的投影,结合图象知,$(a,1)\perp \overrightarrow{AC}$ 及 $(a,1)\perp\overrightarrow{BC}$ 时都满足要求,从而解得 $a=-1$ 或 $a=3$.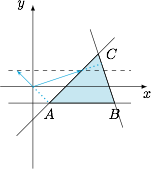

题目
答案
解析
备注