如图,在平面直角坐标系 $xOy$ 中,圆 $C_1:x^2+y^2=4$,圆 $C_2:x^2+y^2=16$,点 $M(1,0)$,动点 $P$、$Q$ 分别在圆 $C_1$ 和圆 $C_2$ 上,满足 $MP\perp MQ$,则线段 $PQ$ 的取值范围是 .

【难度】
【出处】
无
【标注】
【答案】
$\left[\sqrt{19}-1,\sqrt{19}+1\right]$
【解析】
注意到 $MP\perp MQ$,于是可以利用直角三角形斜边上的中线等于斜边的一半来转移线段 $PQ$,这样做的意义在于将两端都在动的线段 $PQ$ 转化成了一端不动($M$)而另一端($E$)运动的线段 $ME$,如图1. 此时需要设法建立 $E$ 点与其他已知条件的联系.连接 $OE$、$OP$、$OQ$,我们可以发现共 $PQ$ 边的三角形 $OPQ$ 和 $MPQ$,而 $OE$ 和 $ME$ 分别是这两个三角形的中线,如图2.
此时需要设法建立 $E$ 点与其他已知条件的联系.连接 $OE$、$OP$、$OQ$,我们可以发现共 $PQ$ 边的三角形 $OPQ$ 和 $MPQ$,而 $OE$ 和 $ME$ 分别是这两个三角形的中线,如图2.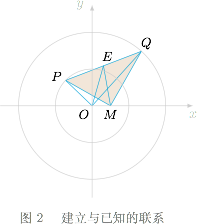 此时根据中线长公式,有$$OP^2+OQ^2=2OE^2+\dfrac 12PQ^2,$$也即$$2OE^2+2ME^2=20,$$这样我们就得到了一个重要的不变量.结合 $OM=1$,由 $OE$、$ME$、$OM$ 的数量关系可得$$(ME-1)^2\leqslant OE^2\leqslant (ME+1)^2,$$因此$$(ME-1)^2+ME^2\leqslant OE^2+ME^2\leqslant (ME+1)^2+ME^2,$$即$$2ME^2-2ME+1\leqslant 10 \leqslant 2ME^2+2ME+1,$$解得$$\dfrac {-1+\sqrt{19}}2\leqslant ME\leqslant \dfrac{1+\sqrt{19}}2,$$从而 $PQ$,也就是 $2ME$ 的取值范围是 $\left[\sqrt{19}-1,\sqrt{19}+1\right]$.
此时根据中线长公式,有$$OP^2+OQ^2=2OE^2+\dfrac 12PQ^2,$$也即$$2OE^2+2ME^2=20,$$这样我们就得到了一个重要的不变量.结合 $OM=1$,由 $OE$、$ME$、$OM$ 的数量关系可得$$(ME-1)^2\leqslant OE^2\leqslant (ME+1)^2,$$因此$$(ME-1)^2+ME^2\leqslant OE^2+ME^2\leqslant (ME+1)^2+ME^2,$$即$$2ME^2-2ME+1\leqslant 10 \leqslant 2ME^2+2ME+1,$$解得$$\dfrac {-1+\sqrt{19}}2\leqslant ME\leqslant \dfrac{1+\sqrt{19}}2,$$从而 $PQ$,也就是 $2ME$ 的取值范围是 $\left[\sqrt{19}-1,\sqrt{19}+1\right]$.
事实上,不变量可以再次利用中线长公式挖掘几何意义.倍长 $ME$ 至 $N$,则$$ON^2+OM^2=2OE^2+\dfrac 12MN^2=2OE^2+2ME^2=20,$$于是 $ON$ 为定长 $\sqrt{19}$,也就是说 $N$ 点的轨迹是以 $O$ 为圆心的圆,如图3.进而 $PQ$,也就是 $MN$ 的取值范围是 $\left[\sqrt{19}-1,\sqrt{19}+1\right]$.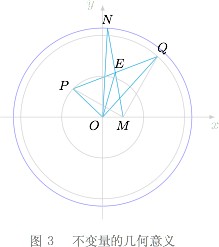
 此时需要设法建立 $E$ 点与其他已知条件的联系.连接 $OE$、$OP$、$OQ$,我们可以发现共 $PQ$ 边的三角形 $OPQ$ 和 $MPQ$,而 $OE$ 和 $ME$ 分别是这两个三角形的中线,如图2.
此时需要设法建立 $E$ 点与其他已知条件的联系.连接 $OE$、$OP$、$OQ$,我们可以发现共 $PQ$ 边的三角形 $OPQ$ 和 $MPQ$,而 $OE$ 和 $ME$ 分别是这两个三角形的中线,如图2. 此时根据中线长公式,有$$OP^2+OQ^2=2OE^2+\dfrac 12PQ^2,$$也即$$2OE^2+2ME^2=20,$$这样我们就得到了一个重要的不变量.结合 $OM=1$,由 $OE$、$ME$、$OM$ 的数量关系可得$$(ME-1)^2\leqslant OE^2\leqslant (ME+1)^2,$$因此$$(ME-1)^2+ME^2\leqslant OE^2+ME^2\leqslant (ME+1)^2+ME^2,$$即$$2ME^2-2ME+1\leqslant 10 \leqslant 2ME^2+2ME+1,$$解得$$\dfrac {-1+\sqrt{19}}2\leqslant ME\leqslant \dfrac{1+\sqrt{19}}2,$$从而 $PQ$,也就是 $2ME$ 的取值范围是 $\left[\sqrt{19}-1,\sqrt{19}+1\right]$.
此时根据中线长公式,有$$OP^2+OQ^2=2OE^2+\dfrac 12PQ^2,$$也即$$2OE^2+2ME^2=20,$$这样我们就得到了一个重要的不变量.结合 $OM=1$,由 $OE$、$ME$、$OM$ 的数量关系可得$$(ME-1)^2\leqslant OE^2\leqslant (ME+1)^2,$$因此$$(ME-1)^2+ME^2\leqslant OE^2+ME^2\leqslant (ME+1)^2+ME^2,$$即$$2ME^2-2ME+1\leqslant 10 \leqslant 2ME^2+2ME+1,$$解得$$\dfrac {-1+\sqrt{19}}2\leqslant ME\leqslant \dfrac{1+\sqrt{19}}2,$$从而 $PQ$,也就是 $2ME$ 的取值范围是 $\left[\sqrt{19}-1,\sqrt{19}+1\right]$.事实上,不变量可以再次利用中线长公式挖掘几何意义.倍长 $ME$ 至 $N$,则$$ON^2+OM^2=2OE^2+\dfrac 12MN^2=2OE^2+2ME^2=20,$$于是 $ON$ 为定长 $\sqrt{19}$,也就是说 $N$ 点的轨迹是以 $O$ 为圆心的圆,如图3.进而 $PQ$,也就是 $MN$ 的取值范围是 $\left[\sqrt{19}-1,\sqrt{19}+1\right]$.

题目
答案
解析
备注