已知平面 $\alpha$ 和 $\beta$ 相交形成的四个二面角的其中一个为 $60^\circ$，则在空间中过某定点 $P$ 与这两个平面所成的线面角均为 $30^\circ$ 的直线 $l$ 条数为 ．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
如图，平面上的两条直线（所成角为 $\theta$）的平分线——为互相垂直的两条直线——在运动过程中始终保持与两条直线所成的角相等，且该角的取值范围分别为 $\left[\dfrac{\theta}2,\dfrac{\pi}2\right]$ 以及 $\left[\dfrac{\pi -\theta}2,\dfrac{\pi}2\right]$．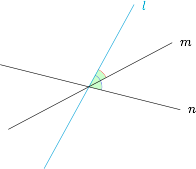
因此当 $\theta=60^\circ$，而与两条直线所成角均为 $60^\circ$ 时对应的直线为 $3$ 条．
因此当 $\theta=60^\circ$，而与两条直线所成角均为 $60^\circ$ 时对应的直线为 $3$ 条．
题目
答案
解析
备注
