将一个水平放置的正方形 $ABCD$ 绕直线 $AB$ 向上转动 $45^\circ$ 到 $ABC_1D_1$，再将所得正方形 $ABC_1D_1$ 绕直线 $BC_1$ 向上转动 $45^\circ$ 到 $A_2BC_1D_2$，则平面 $A_2BC_1D_2$ 与平面 $ABCD$ 所成二面角的正弦值是 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\sqrt 3}2$
【解析】
先考虑三个平面的法向量，可以在正方体中可以作出，分别为 $\overrightarrow{EM},\overrightarrow{EG},\overrightarrow{EN}$，如图：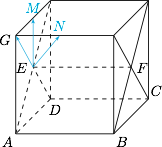
其中 $EM\perp ABCD$，$\angle NEG=45^\circ$，所求角的正弦值即 $\sin\angle MEN$．
由三射线定理知$$\cos\angle MEN=\cos\angle MEG\cos\angle NEG+\sin\angle MEG\sin\angle NEG\cos 90^\circ=\dfrac 12,$$所以 $\sin\angle MEN=\dfrac {\sqrt 3}2$．
其中 $EM\perp ABCD$，$\angle NEG=45^\circ$，所求角的正弦值即 $\sin\angle MEN$．由三射线定理知$$\cos\angle MEN=\cos\angle MEG\cos\angle NEG+\sin\angle MEG\sin\angle NEG\cos 90^\circ=\dfrac 12,$$所以 $\sin\angle MEN=\dfrac {\sqrt 3}2$．
题目
答案
解析
备注
