已知 $AD$ 与 $BC$ 是四面体 $ABCD$ 中互相垂直的棱，若 $BC=2$，$AD=4$，且 $\angle ABD=\angle ACD=60^\circ$，则四面体 $ABCD$ 的体积的最大值是 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{4\sqrt{11}}3$
【解析】
如图，点 $B,C$ 在以 $AD$ 为弦的一个优弧绕 $AD$ 旋转得到的曲面上．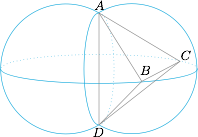
因为四面体 $ABCD$ 的体积$$V_{ABCD}=\dfrac 16\cdot AD\cdot BC\cdot d(AD,BC)\cdot \sin\langle AD,BC\rangle=\dfrac 43d(AD,BC),$$所以当 $d(AD,BC)$ 最大时，有体积的最大值，当 $B,C$ 都在 $AD$ 的中截面上时 $d(AD,BC)$ 有最大值，此时 $BC$ 是一个半径为 $4\cdot\dfrac {\sqrt 3}2=2\sqrt 3$ 的圆的弦，所以圆心到弦心距为 $\sqrt{12-1}=\sqrt {11}$．
因为四面体 $ABCD$ 的体积$$V_{ABCD}=\dfrac 16\cdot AD\cdot BC\cdot d(AD,BC)\cdot \sin\langle AD,BC\rangle=\dfrac 43d(AD,BC),$$所以当 $d(AD,BC)$ 最大时，有体积的最大值，当 $B,C$ 都在 $AD$ 的中截面上时 $d(AD,BC)$ 有最大值，此时 $BC$ 是一个半径为 $4\cdot\dfrac {\sqrt 3}2=2\sqrt 3$ 的圆的弦，所以圆心到弦心距为 $\sqrt{12-1}=\sqrt {11}$．
题目
答案
解析
备注
