若函数 $f(x)=-\ln x+ax^2+bx-a-2b$ 有两个极值点 $x_1,x_2$,其中 $-\dfrac 12<a<0<b$,且 $f\left(x_2\right)=x_2>x_1$,则方程 $2a\left[f(x)\right]^2+bf(x)-1=0$ 的实根个数为 .
【难度】
【出处】
无
【标注】
【答案】
$5$
【解析】
函数 $f(x)$ 的导函数$$f'(x)=\dfrac{2ax^2+bx-1}x,$$于是方程$$2a\left[f(x)\right]^2+bf(x)-1=0$$的实根实际上就是复合函数 $f'\left(f(x)\right)$ 的零点,其处理方法是从外向内逐层“剥开”.
根据以上分析,题中方程等价于$$f(x)=x_1\lor f(x)=x_2,$$因此其实根个数就是函数 $f(x)$ 的图象与直线 $y=x_1$ 以及直线 $y=x_2$ 的交点个数的总和.这样一来,如何准确做出函数 $f(x)$ 的图象成了解决问题的关键. 如图,由 $a<0$ 可以作出 $f'(x)$ 的“示性函数”(决定函数值正负性质的部分因式)$y=2ax^2+bx-1$ 的草图.又函数 $f(x)$ 的定义域为 $(0,+\infty)$,其在区间端点处的函数值 $f(0+)=+\infty$,$f(+\infty)=-\infty$.此外题中告知 $f\left(x_2\right)=x_2>0$.
如图,由 $a<0$ 可以作出 $f'(x)$ 的“示性函数”(决定函数值正负性质的部分因式)$y=2ax^2+bx-1$ 的草图.又函数 $f(x)$ 的定义域为 $(0,+\infty)$,其在区间端点处的函数值 $f(0+)=+\infty$,$f(+\infty)=-\infty$.此外题中告知 $f\left(x_2\right)=x_2>0$.
结合导函数图象与函数在 $0$、$x_2$、$+\infty$ 处的取值可以作出函数 $f(x)$ 的部分图象(缺失极值点 $x=x_1$ 处的信息).据此“残图”可以确定直线 $y=x_2$ 与函数 $f(x)$ 的图象交点数为 $2$.
为了确定函数 $f(x)$ 的图象中残缺的部分,我们需要另外探寻一些特殊点.先考虑方程$$2ax^2+bx-1=0,$$有$$x_1+x_2=-\dfrac b{2a}\land x_1x_2=-\dfrac{1}{2a},$$进而可得$$x_1+x_2\in\left(0,+\infty\right)\land x_1x_2\in\left(1,+\infty\right),$$这样一来,我们可以断定 $x_2>1$,因此选择 $x=1$ 为特殊点进行探索.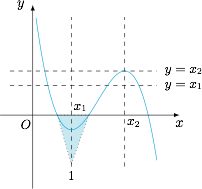 事实上,$f(1)=-b<0$,于是我们“勘探”出在 $x=x_2$ 左侧的未知领域有一片“绿洲”(函数值小于 $0$ 的部分),而 $x=x_1$ 就是这片绿洲的中心小镇.这样就有 $x_1>0>f\left(x_1\right)$,如图.这样直线 $y=x_1$ 与函数 $y=f(x)$ 的图象有 $3$ 个交点.
事实上,$f(1)=-b<0$,于是我们“勘探”出在 $x=x_2$ 左侧的未知领域有一片“绿洲”(函数值小于 $0$ 的部分),而 $x=x_1$ 就是这片绿洲的中心小镇.这样就有 $x_1>0>f\left(x_1\right)$,如图.这样直线 $y=x_1$ 与函数 $y=f(x)$ 的图象有 $3$ 个交点.
综上,题中方程的实根个数为 $5$.
根据以上分析,题中方程等价于$$f(x)=x_1\lor f(x)=x_2,$$因此其实根个数就是函数 $f(x)$ 的图象与直线 $y=x_1$ 以及直线 $y=x_2$ 的交点个数的总和.这样一来,如何准确做出函数 $f(x)$ 的图象成了解决问题的关键.
 如图,由 $a<0$ 可以作出 $f'(x)$ 的“示性函数”(决定函数值正负性质的部分因式)$y=2ax^2+bx-1$ 的草图.又函数 $f(x)$ 的定义域为 $(0,+\infty)$,其在区间端点处的函数值 $f(0+)=+\infty$,$f(+\infty)=-\infty$.此外题中告知 $f\left(x_2\right)=x_2>0$.
如图,由 $a<0$ 可以作出 $f'(x)$ 的“示性函数”(决定函数值正负性质的部分因式)$y=2ax^2+bx-1$ 的草图.又函数 $f(x)$ 的定义域为 $(0,+\infty)$,其在区间端点处的函数值 $f(0+)=+\infty$,$f(+\infty)=-\infty$.此外题中告知 $f\left(x_2\right)=x_2>0$.结合导函数图象与函数在 $0$、$x_2$、$+\infty$ 处的取值可以作出函数 $f(x)$ 的部分图象(缺失极值点 $x=x_1$ 处的信息).据此“残图”可以确定直线 $y=x_2$ 与函数 $f(x)$ 的图象交点数为 $2$.
为了确定函数 $f(x)$ 的图象中残缺的部分,我们需要另外探寻一些特殊点.先考虑方程$$2ax^2+bx-1=0,$$有$$x_1+x_2=-\dfrac b{2a}\land x_1x_2=-\dfrac{1}{2a},$$进而可得$$x_1+x_2\in\left(0,+\infty\right)\land x_1x_2\in\left(1,+\infty\right),$$这样一来,我们可以断定 $x_2>1$,因此选择 $x=1$ 为特殊点进行探索.
 事实上,$f(1)=-b<0$,于是我们“勘探”出在 $x=x_2$ 左侧的未知领域有一片“绿洲”(函数值小于 $0$ 的部分),而 $x=x_1$ 就是这片绿洲的中心小镇.这样就有 $x_1>0>f\left(x_1\right)$,如图.这样直线 $y=x_1$ 与函数 $y=f(x)$ 的图象有 $3$ 个交点.
事实上,$f(1)=-b<0$,于是我们“勘探”出在 $x=x_2$ 左侧的未知领域有一片“绿洲”(函数值小于 $0$ 的部分),而 $x=x_1$ 就是这片绿洲的中心小镇.这样就有 $x_1>0>f\left(x_1\right)$,如图.这样直线 $y=x_1$ 与函数 $y=f(x)$ 的图象有 $3$ 个交点.综上,题中方程的实根个数为 $5$.
题目
答案
解析
备注