已知函数 $f(x)=x^2+{\mathrm e}^x-\dfrac 12,x<0$ 与 $g(x)=x^2+\ln(x+a)$ 的图象上存在关于 $y$ 轴对称的点，则 $a$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$(-\infty,\sqrt{\rm e})$
【解析】
两个函数图象上存在关于 $y$ 轴对称的点，即存在点 $(x,y)$ 与 $(-x,y)$ 分别在两个函数的图象上．不妨设 $x>0$，有$$\begin{cases}y=g(x)=x^2+\ln(x+a),\\y=f(-x)=x^2+{\mathrm e}^{-x}-\frac 12.\end{cases}$$即方程$$\ln(x+a)-{\mathrm e}^{-x}+\frac 12=0$$有正的实数解．考虑将方程的解的问题转化成两个函数的交点问题，方程$$\ln(x+a)={\rm e}^{-x}-\frac 12.$$有正根，即函数 $y=\ln(x+a)$ 与 $y={\rm e}^{-x}-\dfrac 12$ 在 $y$ 轴右侧有交点．如图：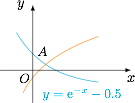
当两个函数图象的交点在 $A\left(0,\dfrac 12\right)$ 的右侧时，满足情况，所以$$a<\sqrt{\rm e}.$$
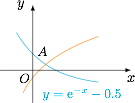当两个函数图象的交点在 $A\left(0,\dfrac 12\right)$ 的右侧时，满足情况，所以$$a<\sqrt{\rm e}.$$
题目
答案
解析
备注
