已知点 $A(-1,1)$，若曲线 $G$ 上存在两点 $B,C$，使得三角形 $ABC$ 为正三角形，则称 $G$ 为 $T$ 型曲线．给定下列三条曲线：
① $y=-x+3(0\leqslant x\leqslant 3)$；
② $y=\sqrt{2-x^2}(-\sqrt{2}\leqslant x\leqslant 0)$；
③ $y=-\dfrac{1}{x}(x>0)$．
则其中是 $T$ 型曲线的为 ．
① $y=-x+3(0\leqslant x\leqslant 3)$；
② $y=\sqrt{2-x^2}(-\sqrt{2}\leqslant x\leqslant 0)$；
③ $y=-\dfrac{1}{x}(x>0)$．
则其中是 $T$ 型曲线的为
【难度】
【出处】
无
【标注】
【答案】
③
【解析】
判定一个三角形为正三角形有很多种方式：三边相等的三角形；有一个角为 $60^\circ$ 的等腰三角形；底边上的高与底边比值为 $\dfrac{\sqrt 3}{2}$ 的等腰三角形等．在动态问题中讨论正三角形的存在性问题时，常常通过利用顶角为 $60^\circ$ 的等腰三角形为正三角形进行判定．
对于 ①，如图，曲线 $G$ 为线段 $MN$，以 $A$ 为圆心作圆与 $G$ 交于两点构成等腰三角形．由于顶点的最大值小于 $60^\circ$，从而不存在满足要求的 $B,C$ 两点；
对于 ②，如图，曲线 $G$ 为一段圆弧，以 $A$ 为圆心作圆与 $G$ 交于两点构成等腰三角形．由于顶角的最小值大于 $60^\circ$，从而不存在满足要求的 $B,C$ 两点；
对于 ③，如图，曲线 $G$ 为反比例曲线在第四象限的部分，以 $A$ 为圆心作圆与 $G$ 交于两点构成等腰三角形．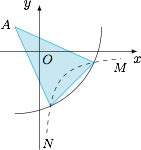
由于顶角 $\angle BAC$ 的范围为 $0^\circ<\angle BAC<90^\circ$，且连续变化，所以存在满足条件的 $B,C$ 两点．
对于 ①，如图，曲线 $G$ 为线段 $MN$，以 $A$ 为圆心作圆与 $G$ 交于两点构成等腰三角形．由于顶点的最大值小于 $60^\circ$，从而不存在满足要求的 $B,C$ 两点；
对于 ②，如图，曲线 $G$ 为一段圆弧，以 $A$ 为圆心作圆与 $G$ 交于两点构成等腰三角形．由于顶角的最小值大于 $60^\circ$，从而不存在满足要求的 $B,C$ 两点；对于 ③，如图，曲线 $G$ 为反比例曲线在第四象限的部分，以 $A$ 为圆心作圆与 $G$ 交于两点构成等腰三角形．由于顶角 $\angle BAC$ 的范围为 $0^\circ<\angle BAC<90^\circ$，且连续变化，所以存在满足条件的 $B,C$ 两点．
题目
答案
解析
备注
