$a$ 为实数，函数 $f\left(x\right)={\left|{x^2-ax}\right|}$ 在区间 $\left[0,1\right]$ 上的最大值记为 $g\left(a\right)$．当 $a=$ 时，$g\left(a\right)$ 的值最小．
【难度】
【出处】
2015年高考湖北卷（文）
【标注】
【答案】
$2\sqrt 2-2$
【解析】
易知函数 $f(x)=|x^2-ax|$ 在 $x=\dfrac a2$ 取得极大值．
当 $\dfrac a2\in [0,1]$ 时，$g(a)$ 为 $f(0)$，$f(1)$ 与 $f\left(\dfrac a2\right)$ 中的最大数，也即$$g(a)=\max\left\{\dfrac{a^2}4,|1-a|\right\},a\in[0,2];$$当 $\dfrac a2\notin [0,1]$ 时，$g(a)$ 为 $f(0)$，$f(1)$ 中的最大数，也即$$g(a)=|1-a|,a\in (-\infty ,0)\cup (2,+\infty ).$$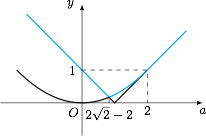
如图，计算函数 $y=|1-a|$ 与函数 $y=\dfrac{a^2}4$ 图象的交点可得 $a=2\sqrt 2-2$（舍去左侧交点）．
因此当 $a=2\sqrt 2-2$ 时，$g(a)$ 的值最小．
当 $\dfrac a2\in [0,1]$ 时，$g(a)$ 为 $f(0)$，$f(1)$ 与 $f\left(\dfrac a2\right)$ 中的最大数，也即$$g(a)=\max\left\{\dfrac{a^2}4,|1-a|\right\},a\in[0,2];$$当 $\dfrac a2\notin [0,1]$ 时，$g(a)$ 为 $f(0)$，$f(1)$ 中的最大数，也即$$g(a)=|1-a|,a\in (-\infty ,0)\cup (2,+\infty ).$$
如图，计算函数 $y=|1-a|$ 与函数 $y=\dfrac{a^2}4$ 图象的交点可得 $a=2\sqrt 2-2$（舍去左侧交点）．因此当 $a=2\sqrt 2-2$ 时，$g(a)$ 的值最小．
题目
答案
解析
备注
