以下是面点师一个工作环节的数学模型：如图，在数轴上截取与闭区间 $[0,4]$ 对应的线段，对折后（坐标 $4$ 对应的点与原点重合）再均匀地拉成 $4$ 个单位长度的线段，这一过程称为一次操作（例如在第一次操作完成后，原来的坐标 $1$、$3$ 变成 $2$，原来的坐标 $2$ 变成 $4$，等等）．
那么原闭区间 $[0,4]$ 上（除两个端点外）的点，在第 $n$ 次操作完成后（$n\geqslant 1$），恰好被拉到与 $4$ 重合的点所对应的坐标为 $f(n)$，则 $f(3)=$ ，$f(n)=$ ．
那么原闭区间 $[0,4]$ 上（除两个端点外）的点，在第 $n$ 次操作完成后（$n\geqslant 1$），恰好被拉到与 $4$ 重合的点所对应的坐标为 $f(n)$，则 $f(3)=$ 【难度】
【出处】
无
【标注】
【答案】
$\dfrac 12,\dfrac 32,\dfrac 52,\dfrac 72$；$\dfrac {1}{2^{n-2}},\dfrac {3}{2^{n-2}},\dfrac {5}{2^{n-2}},\cdots,\dfrac {2^{n}-1}{2^{n-2}}$
【解析】
本题的关键是将这个数学模型每次对折再拉伸的过程中每个点的坐标变化想明白，对于闭区间上的每个点 $x$，对折并拉伸会对应到唯一的一个新的坐标 $y$，所以可以用函数 $y=g(x)$ 去表示一次对折与拉伸后对应的关系，比如有 $g(2)=4,g(4)=0$．容易知道第一次对折拉伸后，得到的函数解析式为$$g(x)=\begin{cases} 2x,x\in[0,2],\\2(4-x),x\in(2,4].\end{cases}$$图象如下：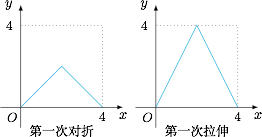
每一次对折拉伸都将 $x$ 对应到 $g(x)$，所以第二次对折拉伸后 $x$ 对应到 $g\big(g(x)\big)$，第三次对折拉伸后 $x$ 对应到 $g\big[g\big(g(x)\big)\big]$，$\cdots$．其中 $g\big(g(x)\big)$ 与 $g\big[g\big(g(x)\big)\big]$ 的图象如下：
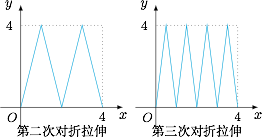$g\big[g\big(g(x)\big)\big]=4$ 的解（除 $0,4$ 外）即 $f(3)$ 的值，故为 $\dfrac 12,\dfrac 32,\dfrac 52,\dfrac 72$．
我们容易得到图象的变化规律，从而可以归纳得到$$f(n)=\dfrac {1}{2^{n-2}},\dfrac {3}{2^{n-2}},\dfrac {5}{2^{n-2}},\cdots,\dfrac {2^{n}-1}{2^{n-2}}.$$重复操作的过程对于函数或数列来说，就是递推或迭代的过程，想明白这样的过程就会将复杂的步骤化成一步步简单的过程的迭加．
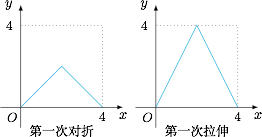每一次对折拉伸都将 $x$ 对应到 $g(x)$，所以第二次对折拉伸后 $x$ 对应到 $g\big(g(x)\big)$，第三次对折拉伸后 $x$ 对应到 $g\big[g\big(g(x)\big)\big]$，$\cdots$．其中 $g\big(g(x)\big)$ 与 $g\big[g\big(g(x)\big)\big]$ 的图象如下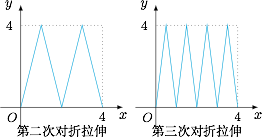：$g\big[g\big(g(x)\big)\big]=4$ 的解（除 $0,4$ 外）即 $f(3)$ 的值，故为 $\dfrac 12,\dfrac 32,\dfrac 52,\dfrac 72$．我们容易得到图象的变化规律，从而可以归纳得到$$f(n)=\dfrac {1}{2^{n-2}},\dfrac {3}{2^{n-2}},\dfrac {5}{2^{n-2}},\cdots,\dfrac {2^{n}-1}{2^{n-2}}.$$重复操作的过程对于函数或数列来说，就是递推或迭代的过程，想明白这样的过程就会将复杂的步骤化成一步步简单的过程的迭加．
题目
答案
解析
备注
