已知函数 $f(x)=\begin{cases} -x^2+2x,x\geqslant 0,\\x^2-2x,x<0\end{cases}$，若关于 $x$ 的不等式 $[f(x)]^2+af(x)-b^2<0$ 恰有一个整数解，则实数 $a$ 的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$8$
【解析】
令 $t=f(x)$，则题中不等式转化成 $t^2+at-b^2<0$，由题意知此不等式一定有解，由不等式的形式知，解集可设为 $(t_1,t_2)$，且有$$t_1+t_2=-a,t_1t_2=-b^2\leqslant 0.$$于是问题转化为 $t_1<f(x)<t_2$ 恰有一个整数解，即函数 $y=f(x)$ 的图象在直线 $y=t_1$ 与 $y=t_2$ 之间的部分（不包含边界）对应的横坐标中只有一个整数．作出 $y=f(x)$ 的图象，如下：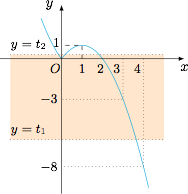
因为 $t_1\leqslant 0\leqslant t_2$，要使得点 $(0,0),(2,0)$ 不在阴影部分内，需要上下边界中至少有一个恰为 $x$ 轴（也可以从代数角度考虑，因为 $f(0)=f(2)=0$，要使得不等式只有一个整数解，必须有 $b=0$）．要求的值为 $a$ 的最大值，所以先考虑 $a>0$ 的情况，此时$$t_1=-a<0,t_2=0,$$结合 $f(x)$ 的图象知$$t_1=-a\in[-8,-3),$$即 $a\in(3,8]$，故 $a$ 的最大值为 $8$．
因为 $t_1\leqslant 0\leqslant t_2$，要使得点 $(0,0),(2,0)$ 不在阴影部分内，需要上下边界中至少有一个恰为 $x$ 轴（也可以从代数角度考虑，因为 $f(0)=f(2)=0$，要使得不等式只有一个整数解，必须有 $b=0$）．要求的值为 $a$ 的最大值，所以先考虑 $a>0$ 的情况，此时$$t_1=-a<0,t_2=0,$$结合 $f(x)$ 的图象知$$t_1=-a\in[-8,-3),$$即 $a\in(3,8]$，故 $a$ 的最大值为 $8$．
题目
答案
解析
备注
