设变量 $x,y$ 满足约束条件 $\begin{cases} y-1\geqslant 0,\\x+y-4\leqslant 0,\\y-1\leqslant k(x-1),\end{cases}$ 其中 $k\in\mathbb{R}$，$k>0$．当 $k=1$ 时，$\dfrac {y}{x^2}$ 的最大值为 ；若 $\dfrac {y}{x^2}$ 的最大值为 $1$，则实数 $k$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$1$；$(0,2]$
【解析】
对于规划问题，关键是分析可行域与目标函数．
首先看可行域，在本题中，可行域是一个三角形，$A(1,1),B(3,1)$ 是它的两个固定的顶点，另外一个顶点 $C$ 随着 $k$ 的变化而变化．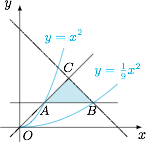
记 $m=\dfrac {y}{x^2}$，则 $y=mx^2,m>0$ 表示以 $y$ 轴为对称轴、开口向上的抛物线，当 $m$ 的值增大时，抛物线 $y=mx^2$ 离 $y$ 轴的距离越来越近．
于是我们得到，当 $k=1$ 时，$\dfrac{y}{x^2}$ 的最大值为 $1$；
如果 $\dfrac {y}{x^2}$ 的最大值为 $1$，说明 $\triangle ABC$ 中所有的点都在抛物线的外部（指抛物线不包含焦点的部分），如图：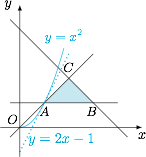
这就需要直线 $AC$ 的斜率 $k$ 不超过抛物线 $y=x^2$ 在点 $A(1,1)$ 处的切线的斜率 $y'|_{x=1}=2$，从而得到 $k\in(0,2]$．
首先看可行域，在本题中，可行域是一个三角形，$A(1,1),B(3,1)$ 是它的两个固定的顶点，另外一个顶点 $C$ 随着 $k$ 的变化而变化．
记 $m=\dfrac {y}{x^2}$，则 $y=mx^2,m>0$ 表示以 $y$ 轴为对称轴、开口向上的抛物线，当 $m$ 的值增大时，抛物线 $y=mx^2$ 离 $y$ 轴的距离越来越近．于是我们得到，当 $k=1$ 时，$\dfrac{y}{x^2}$ 的最大值为 $1$；
如果 $\dfrac {y}{x^2}$ 的最大值为 $1$，说明 $\triangle ABC$ 中所有的点都在抛物线的外部（指抛物线不包含焦点的部分），如图：
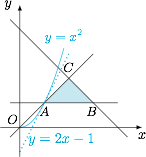这就需要直线 $AC$ 的斜率 $k$ 不超过抛物线 $y=x^2$ 在点 $A(1,1)$ 处的切线的斜率 $y'|_{x=1}=2$，从而得到 $k\in(0,2]$．
题目
答案
解析
备注
