查看数据源：59102a5540fdc700073df4f1
在平面直角坐标系 $xOy$ 中，$O$ 为坐标原点．定义 $P(x_1,y_1)$、$Q(x_2,y_2)$ 两点之间的“折线距离”为 $d(P,Q)=|x_1-x_2|+|y_1-y_2|$．
$(1)$ 若点 $A(-1,3)$，则 $d(A,O)=$  ；
$(2)$ 已知点 $ B(1,0)$，点 $ M $ 是直线 $ l $：$ kx-y+k+3=0(k>0)$ 上的动点，$ d(B,M)$ 的最小值为 ；
$(3)$ 圆 $ x^2+y^2=1 $ 上一点与直线 $ m $：$ 2x+y-2\sqrt 5=0$ 上一点的“折线距离”的最小值是 ．
【难度】
【出处】
无
【标注】
  • 题型
    >
    解析几何
    >
    解析几何创新题
  • 方法
    >
    思考方式
    >
    信息迁移
【答案】
$(1)$ $4$；$(2)$ $\begin{cases}2k+3,0<k\leqslant 1,\\\dfrac 3k+2,k>1\end{cases}$；$(3)$ $\dfrac {\sqrt 5}{2}$
【解析】
用图形语言理解折线距离 $d(A,B)$，其本质就是从 $A$ 到 $B$ 只能沿竖直方向和水平方向分别移动的折线的最小长度，如图两种颜色的折线路径都对应 $A,B$ 的折线距离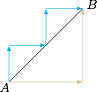：$(1)$ 根据折线距离的概念知$$d(A,O)=|-1|+|3|=4;$$$(2)$ 直线 $l$ 即$$y=k(x+1)+3,$$是过定点 $C(-1,3)$ 的直线系．先来确定点 $M$ 的位置：
过 $B$ 作水平线与竖直线分别交直线 $l$ 于$$S\left(-\dfrac 3k-1,0\right),T(1,2k+3),$$如图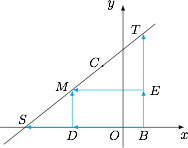：当点 $M$ 在 $S$ 左下方时，有$$d(B,M)>d(B,S)=|BS|.$$当点 $M$ 在 $T$ 右上方时，有$$d(B,M)>d(B,T)=|BT|.$$当点 $M$ 在线段 $ST$ 上（包括端点）时，有$$d(B,M)=|BD|+|DM|=|BE|+|EM|,$$其中 $D$ 为 $M$ 在 $BS$ 上的投影，$E$ 为 $M$ 在 $BT$ 上的投影．
当 $0<k<1$ 时，有 $|EM|\geqslant |ET|$，从而$$d(B,M)\geqslant |BE|+|ET|=|BT|=d(B,T);$$当 $k\geqslant 1$ 时，有 $|DM|\geqslant |DS|$，从而$$d(B,M)\geqslant |BD|+|DS|=|BS|=d(B,S).$$因此 $d(B,M)$ 的最小值为$$\begin{cases} d(B,T)=2k+3,0<k<1,\\d(B,S)=\dfrac 3k+2,k\geqslant 1.\end{cases}$$$(3)$ 在 $(2)$ 中我们知道，定点到直线上一点的折线距离的最小值等于该点到直线的水平距离或竖直距离中较小的．
因为直线 $m$ 的斜率为 $-2$，于是点 $M$ 到直线 $m$ 的折线距离的最小值即 $M$ 到直线 $m$ 的水平距离，如图：当点 $M$ 在单位圆上运动时，点 $M$ 到直线 $m$ 的水平距离的最小值为 $\dfrac{\sqrt {5}}{2}$．
题目 答案 解析 备注
0.107922s