在平面直角坐标系中,如果 $x$ 和 $y$ 都是整数,就称点 $(x,y)$ 是整点,下列命题中正确的是 (写出所有正确命题的编号).
① 存在这样的直线,既不与坐标轴平行又不经过任何整点;
② 如果 $k$ 与 $b$ 都是无理数,则直线 $y=kx+b$ 不经过任何整点;
③ 直线 $l$ 经过无穷多个整点,当且仅当 $l$ 经过两个不同的整点;
④ 直线 $y=kx+b$ 经过无穷多个整点的充分必要条件是:$k$ 与 $b$ 都是有理数;
⑤ 存在恰经过一个整点的直线.
① 存在这样的直线,既不与坐标轴平行又不经过任何整点;
② 如果 $k$ 与 $b$ 都是无理数,则直线 $y=kx+b$ 不经过任何整点;
③ 直线 $l$ 经过无穷多个整点,当且仅当 $l$ 经过两个不同的整点;
④ 直线 $y=kx+b$ 经过无穷多个整点的充分必要条件是:$k$ 与 $b$ 都是有理数;
⑤ 存在恰经过一个整点的直线.
【难度】
【出处】
2011年高考安徽卷(理)
【标注】
【答案】
①③⑤
【解析】
这道题是整点问题,画出平面直角坐标系中的整点,从几何与代数两方面去考虑这几个结论的正确性.对于不成立的结论,只要举出反例即可,对于成立的结论则需要给出证明.
考虑 ①,画出原点附近的整点,如图的直线既不与坐标轴平行,又不经过任何整点,比如直线 $y=x+\dfrac 12$,这样的直线有无穷多条,① 成立;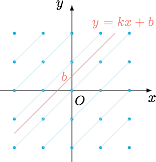 考虑 ②,$k$ 为斜率,$b$ 为纵截距,在 $y$ 轴上任取一个纵坐标为无理数的点,考虑这个点与任何一个整点(不在 $y$ 轴上)的连线,则该直线的斜率一定为无理数,但这条直线上有且仅有一个整点.例如过 $(0,\sqrt 2)$ 与 $(1,0)$ 的直线$$y=\sqrt 2(1-x),$$故 ② 不正确,⑤ 正确,对于 ⑤ 也可以考虑过任意一个整点,且斜率为无理数的直线,这条直线上一定没有其它整点,否则两个整点的连线对应的斜率必为有理数,故 ⑤ 正确;
考虑 ②,$k$ 为斜率,$b$ 为纵截距,在 $y$ 轴上任取一个纵坐标为无理数的点,考虑这个点与任何一个整点(不在 $y$ 轴上)的连线,则该直线的斜率一定为无理数,但这条直线上有且仅有一个整点.例如过 $(0,\sqrt 2)$ 与 $(1,0)$ 的直线$$y=\sqrt 2(1-x),$$故 ② 不正确,⑤ 正确,对于 ⑤ 也可以考虑过任意一个整点,且斜率为无理数的直线,这条直线上一定没有其它整点,否则两个整点的连线对应的斜率必为有理数,故 ⑤ 正确;
考虑 ③,当直线 $l$ 经过两个不同的整点 $A,B$ 时,点 $A$ 关于点 $B$ 的对称点,以及点 $B$ 关于点 $A$ 的对称点一定都是整点,且在直线 $l$ 上,类似这样的对称可以一直进行下去,所以 $l$ 一定经过无穷多个整点.反之显然,故 ③ 成立.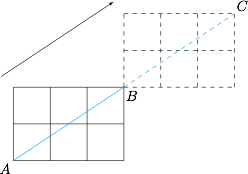 考虑 ④,当 $y=kx+b$ 经过无穷多个整点时,由斜率公式知 $k$ 为有理数,从而 $b=y-kx$ 为有理数;反之,$k,b$ 都是有理数时,可以不经过任何整点,如 ① 中的例子 $y=x+\dfrac 12$,故 ④ 错误.
考虑 ④,当 $y=kx+b$ 经过无穷多个整点时,由斜率公式知 $k$ 为有理数,从而 $b=y-kx$ 为有理数;反之,$k,b$ 都是有理数时,可以不经过任何整点,如 ① 中的例子 $y=x+\dfrac 12$,故 ④ 错误.
综上,正确的命题为 ①③⑤.
考虑 ①,画出原点附近的整点,如图的直线既不与坐标轴平行,又不经过任何整点,比如直线 $y=x+\dfrac 12$,这样的直线有无穷多条,① 成立;
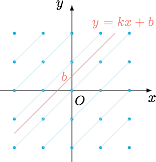 考虑 ②,$k$ 为斜率,$b$ 为纵截距,在 $y$ 轴上任取一个纵坐标为无理数的点,考虑这个点与任何一个整点(不在 $y$ 轴上)的连线,则该直线的斜率一定为无理数,但这条直线上有且仅有一个整点.例如过 $(0,\sqrt 2)$ 与 $(1,0)$ 的直线$$y=\sqrt 2(1-x),$$故 ② 不正确,⑤ 正确,对于 ⑤ 也可以考虑过任意一个整点,且斜率为无理数的直线,这条直线上一定没有其它整点,否则两个整点的连线对应的斜率必为有理数,故 ⑤ 正确;
考虑 ②,$k$ 为斜率,$b$ 为纵截距,在 $y$ 轴上任取一个纵坐标为无理数的点,考虑这个点与任何一个整点(不在 $y$ 轴上)的连线,则该直线的斜率一定为无理数,但这条直线上有且仅有一个整点.例如过 $(0,\sqrt 2)$ 与 $(1,0)$ 的直线$$y=\sqrt 2(1-x),$$故 ② 不正确,⑤ 正确,对于 ⑤ 也可以考虑过任意一个整点,且斜率为无理数的直线,这条直线上一定没有其它整点,否则两个整点的连线对应的斜率必为有理数,故 ⑤ 正确;考虑 ③,当直线 $l$ 经过两个不同的整点 $A,B$ 时,点 $A$ 关于点 $B$ 的对称点,以及点 $B$ 关于点 $A$ 的对称点一定都是整点,且在直线 $l$ 上,类似这样的对称可以一直进行下去,所以 $l$ 一定经过无穷多个整点.反之显然,故 ③ 成立.
 考虑 ④,当 $y=kx+b$ 经过无穷多个整点时,由斜率公式知 $k$ 为有理数,从而 $b=y-kx$ 为有理数;反之,$k,b$ 都是有理数时,可以不经过任何整点,如 ① 中的例子 $y=x+\dfrac 12$,故 ④ 错误.
考虑 ④,当 $y=kx+b$ 经过无穷多个整点时,由斜率公式知 $k$ 为有理数,从而 $b=y-kx$ 为有理数;反之,$k,b$ 都是有理数时,可以不经过任何整点,如 ① 中的例子 $y=x+\dfrac 12$,故 ④ 错误.综上,正确的命题为 ①③⑤.
题目
答案
解析
备注