在平面直角坐标系中，已知点 $F(3,0)$ 在圆 $C:(x-m)^2+(y-2)^2=40$ 内，动直线 $AB$ 过点 $F$ 且交圆于 $A,B$ 两点，若 $\triangle ABC$ 的面积的最大值为 $20$，则实数 $m$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$(-3,-1]\cup [7,9)$
【解析】
注意到 $\triangle ABC$ 是以弦 $AB$ 为底，圆 $C$ 的半径为腰的等腰三角形．于是可得当 $\triangle ABC$ 的面积取得最大值 $20$ 时，其顶角 $\angle ACB$ 为直角，进而将条件“挪移”为圆心 $C$ 到直线 $AB$ 的距离为半径的 $\dfrac{1}{\sqrt 2}$，也即直线 $AB$ 是圆$$(x-m)^2+(y-2)^2=20$$的切线，如图．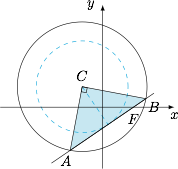
因此题意即过点 $F$ 可以作圆$$(x-m)^2+(y-2)^2=20$$的切线，即$$20\leqslant (3-m)^2+(0-2)^2<40,$$解得 $m$ 的取值范围是 $(-3,-1]\cup [7,9)$．
因此题意即过点 $F$ 可以作圆$$(x-m)^2+(y-2)^2=20$$的切线，即$$20\leqslant (3-m)^2+(0-2)^2<40,$$解得 $m$ 的取值范围是 $(-3,-1]\cup [7,9)$．
题目
答案
解析
备注
