在圆 $x^2+y^2=25$ 上有一点 $P(4,3)$，点 $E,F$ 是 $y$ 轴上两点，且满足 $|PE|=|PF|$，直线 $PE,PF$ 与圆交于 $C,D$，则直线 $CD$ 的斜率是 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac 43$
【解析】
当点 $E,F$ 在 $y$ 轴上运动时，直线 $CD$ 的斜率不变．
过 $P$ 作 $x$ 轴的平行线，交圆 $O$ 于 $Q$，连接 $OQ,CQ,DQ$，如图：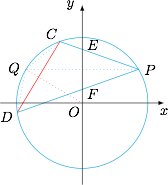
我们知道$$\angle CPQ=\angle DPQ,$$从而有$$CQ=DQ,$$即 $Q$ 点平分弧 $CD$，故有$$OQ\perp CD,$$而 $Q(-4,3)$，故$$k_{CD}=-\dfrac {1}{k_{OQ}}=\dfrac 43.$$当点 $E,F$ 越来越靠近时，点 $C,D$ 趋向于 $Q$ 点，直线 $CD$ 的极限情况是圆在点 $Q$ 处的切线．
过 $P$ 作 $x$ 轴的平行线，交圆 $O$ 于 $Q$，连接 $OQ,CQ,DQ$，如图：
我们知道$$\angle CPQ=\angle DPQ,$$从而有$$CQ=DQ,$$即 $Q$ 点平分弧 $CD$，故有$$OQ\perp CD,$$而 $Q(-4,3)$，故$$k_{CD}=-\dfrac {1}{k_{OQ}}=\dfrac 43.$$当点 $E,F$ 越来越靠近时，点 $C,D$ 趋向于 $Q$ 点，直线 $CD$ 的极限情况是圆在点 $Q$ 处的切线．
题目
答案
解析
备注
