在长方体 $ABCD-A_1B_1C_1D_1$ 中,$AB=BC=2$,$AA_1=1$,$E$、$F$ 为对角线 $BD_1$ 的两个三等分点,$G$ 为长方体表面上的动点,则 $\angle EGF$ 的最大值为 .

【难度】
【出处】
无
【标注】
【答案】
$90^{\circ}$
【解析】
显然线段 $EF$ 是定长的线段,长度为$$\dfrac 13\sqrt{2^2+2^2+1}=1.$$我们知道,在平面上对定长的线段所张的角为定角的点的轨迹是两段圆弧,即“等张角线”.如图1,在平面等张角线逐步扩张的过程中,对应的定角逐步减小(可以由正弦定理推得). 于是空间的等张角线如图2所示,由圆弧绕线段旋转而成,类似于“橄榄”到球体再到“南瓜”,它的任何一个轴截面都是平面等张角线.
于是空间的等张角线如图2所示,由圆弧绕线段旋转而成,类似于“橄榄”到球体再到“南瓜”,它的任何一个轴截面都是平面等张角线.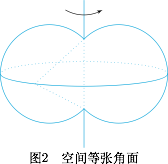 回到原问题,想象一个“橄榄”(从线段 $EF$ 开始)逐步膨胀(到球再到“南瓜),在膨胀过程中,空间等张角面对应的定角持续减小,因此第一次和长方体的表面相切时,切点就是使得 $\angle EGF$ 最大的 $G$ 点的位置.
回到原问题,想象一个“橄榄”(从线段 $EF$ 开始)逐步膨胀(到球再到“南瓜),在膨胀过程中,空间等张角面对应的定角持续减小,因此第一次和长方体的表面相切时,切点就是使得 $\angle EGF$ 最大的 $G$ 点的位置.
接下来,由于长方体和空间等张角面均关于线段 $EF$ 的中点对称,于是空间等张角面会依次与长方体的三组对面相切,并且切点在长方体的某个对角面上,因此逐一分析对角面 $BDD_1B_1$、$A_1BCD_1$、$ABC_1D_1$ 的情形即可,如图3.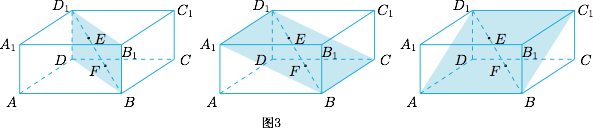 如图4,对角面 $BDD_1B_1$ 对应的切点为上下底面的中心,所得的 $\angle EGF=90^\circ$,此时空间等张角面为球面;
如图4,对角面 $BDD_1B_1$ 对应的切点为上下底面的中心,所得的 $\angle EGF=90^\circ$,此时空间等张角面为球面; 如图5,对角面 $A_1BCD_1$ 对应的切点分别在面对角线 $A_1B$ 和 $D_1C$ 上,所得 $\angle EGF<90^\circ$,此时空间等张角面是南瓜面;与此同时对角面 $ABC_1D_1$ 的边 $AD_1$ 和 $BC_1$ 上也有切点.
如图5,对角面 $A_1BCD_1$ 对应的切点分别在面对角线 $A_1B$ 和 $D_1C$ 上,所得 $\angle EGF<90^\circ$,此时空间等张角面是南瓜面;与此同时对角面 $ABC_1D_1$ 的边 $AD_1$ 和 $BC_1$ 上也有切点. 综上,所求 $\angle EGF$ 的最大值为 $90^\circ$,当且仅当 $G$ 位于上下底面的中心时取得最大值.
综上,所求 $\angle EGF$ 的最大值为 $90^\circ$,当且仅当 $G$ 位于上下底面的中心时取得最大值.
 于是空间的等张角线如图2所示,由圆弧绕线段旋转而成,类似于“橄榄”到球体再到“南瓜”,它的任何一个轴截面都是平面等张角线.
于是空间的等张角线如图2所示,由圆弧绕线段旋转而成,类似于“橄榄”到球体再到“南瓜”,它的任何一个轴截面都是平面等张角线. 回到原问题,想象一个“橄榄”(从线段 $EF$ 开始)逐步膨胀(到球再到“南瓜),在膨胀过程中,空间等张角面对应的定角持续减小,因此第一次和长方体的表面相切时,切点就是使得 $\angle EGF$ 最大的 $G$ 点的位置.
回到原问题,想象一个“橄榄”(从线段 $EF$ 开始)逐步膨胀(到球再到“南瓜),在膨胀过程中,空间等张角面对应的定角持续减小,因此第一次和长方体的表面相切时,切点就是使得 $\angle EGF$ 最大的 $G$ 点的位置.接下来,由于长方体和空间等张角面均关于线段 $EF$ 的中点对称,于是空间等张角面会依次与长方体的三组对面相切,并且切点在长方体的某个对角面上,因此逐一分析对角面 $BDD_1B_1$、$A_1BCD_1$、$ABC_1D_1$ 的情形即可,如图3.
 如图4,对角面 $BDD_1B_1$ 对应的切点为上下底面的中心,所得的 $\angle EGF=90^\circ$,此时空间等张角面为球面;
如图4,对角面 $BDD_1B_1$ 对应的切点为上下底面的中心,所得的 $\angle EGF=90^\circ$,此时空间等张角面为球面; 如图5,对角面 $A_1BCD_1$ 对应的切点分别在面对角线 $A_1B$ 和 $D_1C$ 上,所得 $\angle EGF<90^\circ$,此时空间等张角面是南瓜面;与此同时对角面 $ABC_1D_1$ 的边 $AD_1$ 和 $BC_1$ 上也有切点.
如图5,对角面 $A_1BCD_1$ 对应的切点分别在面对角线 $A_1B$ 和 $D_1C$ 上,所得 $\angle EGF<90^\circ$,此时空间等张角面是南瓜面;与此同时对角面 $ABC_1D_1$ 的边 $AD_1$ 和 $BC_1$ 上也有切点. 综上,所求 $\angle EGF$ 的最大值为 $90^\circ$,当且仅当 $G$ 位于上下底面的中心时取得最大值.
综上,所求 $\angle EGF$ 的最大值为 $90^\circ$,当且仅当 $G$ 位于上下底面的中心时取得最大值.
题目
答案
解析
备注