已知 $\mathbb{R}$ 上的奇函数 $f(x)$ 满足 $f'(x)>-2$，则不等式$$f(x-1)<x^2\left(3-2\ln x \right) +3(1-2x)$$的解集是 ．
【难度】
【出处】
无
【标注】
【答案】
$(0,1)$
【解析】
所解不等式左边是一个抽象函数，我们需要充分利用题目所给条件：$f(x)$ 为奇函数，且 $f'(x)>-2$．
于是我们令 $g(x)=f(x)+2x$，则函数 $g(x)$ 为 $\mathbb R$ 上的单调递增函数，且 $g(0)=0$．
根据题意，将不等式整理为$$f(x-1)+2(x-1)<3x^2-4x+1-2x^2\ln x,$$即$$g(x-1)<3x^2-4x+1-2x^2\ln x.$$下面我们来研究右边的函数的性质，因为有对数函数，所以我们先将右面变形为 $x^2\left(3-\dfrac 4x+\dfrac 1{x^2}-2\ln x\right)$，令$$h(x)=3-\dfrac 4x+\dfrac 1{x^2}-2\ln x,$$则 $h(x)$ 的导函数$$h'(x)=-\dfrac{2(x-1)^2}{x^3}\leqslant 0,$$于是 $h(x)$ 单调递减，又注意到 $h(1)=0$，于是当 $0<x<1$ 时，$g(x-1)<0<x^2\cdot h(x)$；当 $x \geqslant 1$ 时，$x^2\cdot h(x)\leqslant 0\leqslant g(x-1)$．示意图如下：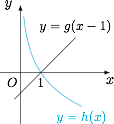
综上，所求的解集为 $(0,1)$．
于是我们令 $g(x)=f(x)+2x$，则函数 $g(x)$ 为 $\mathbb R$ 上的单调递增函数，且 $g(0)=0$．
根据题意，将不等式整理为$$f(x-1)+2(x-1)<3x^2-4x+1-2x^2\ln x,$$即$$g(x-1)<3x^2-4x+1-2x^2\ln x.$$下面我们来研究右边的函数的性质，因为有对数函数，所以我们先将右面变形为 $x^2\left(3-\dfrac 4x+\dfrac 1{x^2}-2\ln x\right)$，令$$h(x)=3-\dfrac 4x+\dfrac 1{x^2}-2\ln x,$$则 $h(x)$ 的导函数$$h'(x)=-\dfrac{2(x-1)^2}{x^3}\leqslant 0,$$于是 $h(x)$ 单调递减，又注意到 $h(1)=0$，于是当 $0<x<1$ 时，$g(x-1)<0<x^2\cdot h(x)$；当 $x \geqslant 1$ 时，$x^2\cdot h(x)\leqslant 0\leqslant g(x-1)$．示意图如下：
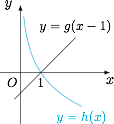综上，所求的解集为 $(0,1)$．
题目
答案
解析
备注
