平面内定义“区域 $X$”为满足条件 $P$ 的所有线段所在的区域．如：平面直角坐标系中，若条件 $P$ 为“线段的一端在原点，另一端距离原点不超过 $1$ 个单位”，则其对应的“区域 $X$”为满足 $x^2+y^2\leqslant 1$ 的区域．
若平面内有夹角成 $60^\circ$ 的两条直线 $l_{OA}$ 与 $l_{OB}$，且两直线交于 $O$，$C,D$ 分别为 $l_{OA}$ 与 $l_{OB}$ 上的点，并满足条件 $P$：$|OC|\cdot |OD|=4$，$E$ 为线段 $CD$ 的中点，记所有线段 $CD$ 所在区域为“区域 $X$”．试判断：
① $I$ 为 $\angle AOB$ 的角平分线上一点，且 $|OI|=2$，以 $I$ 为圆心，$2-\sqrt 3$ 为半径作圆，则该圆上的点均不在“区域 $X$”内；
② $E$ 在“区域 $X$”内，且 $|OE|_{\min}=\sqrt 3$；
③ 过 $E$ 作 $EM\perp OA$ 于 $M$，$EN\perp OB$ 于点 $N$，记 $\triangle MNE$ 的面积为 $S_1$，过 $E$ 作 $EF\parallel l_{OA}$ 交 $l_{OB}$ 于 $F$，$EG\parallel l_{OB}$ 交 $l_{OA}$ 于 $G$，记 $\triangle OFG$ 的面积为 $S_2$，则 $S_1\leqslant S_2$ 恒成立；
④ 存在有限条直线 $l$，使得整条 $l$ 在“区域 $X$ "内．
其中正确的有 ．
若平面内有夹角成 $60^\circ$ 的两条直线 $l_{OA}$ 与 $l_{OB}$，且两直线交于 $O$，$C,D$ 分别为 $l_{OA}$ 与 $l_{OB}$ 上的点，并满足条件 $P$：$|OC|\cdot |OD|=4$，$E$ 为线段 $CD$ 的中点，记所有线段 $CD$ 所在区域为“区域 $X$”．试判断：
① $I$ 为 $\angle AOB$ 的角平分线上一点，且 $|OI|=2$，以 $I$ 为圆心，$2-\sqrt 3$ 为半径作圆，则该圆上的点均不在“区域 $X$”内；
② $E$ 在“区域 $X$”内，且 $|OE|_{\min}=\sqrt 3$；
③ 过 $E$ 作 $EM\perp OA$ 于 $M$，$EN\perp OB$ 于点 $N$，记 $\triangle MNE$ 的面积为 $S_1$，过 $E$ 作 $EF\parallel l_{OA}$ 交 $l_{OB}$ 于 $F$，$EG\parallel l_{OB}$ 交 $l_{OA}$ 于 $G$，记 $\triangle OFG$ 的面积为 $S_2$，则 $S_1\leqslant S_2$ 恒成立；
④ 存在有限条直线 $l$，使得整条 $l$ 在“区域 $X$ "内．
其中正确的有
【难度】
【出处】
无
【标注】
【答案】
③
【解析】
我们知道，如果 $C,D$ 在两条互相垂直的直线（不妨设在 $x$ 轴与 $y$ 轴）上运动，且有 $|OC|\cdot |OD|=4$，则它们的中点 $E$ 的轨迹为两对双曲线 $xy=\pm 1$．而线段所在的区域为以这两对双曲线为边界的“四角星”区域，但不包含原点，如图：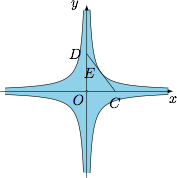
现在两条互相垂直的直线变成了夹角为 $60^\circ$ 的两条直线，我们猜测点 $E$ 的轨迹仍然为两条双曲线，下面给出严格推导：
以 $l_{OA},l_{OB}$ 的两条角平分线为坐标轴建立直角坐标系，使得 $\angle xOA=\angle xOB=30^\circ $，先考虑点 $C$、$D$ 分别在第一、四象限时点 $E$ 的轨迹：
设 $|OC|=r$，则 $|OD|=\dfrac {4}{r}$，于是$$C\left(\dfrac{\sqrt 3}{2}r,\dfrac 12 r\right ),D\left(\dfrac{\sqrt 3}{2}\cdot \dfrac{4}{r},-\dfrac 12\cdot\dfrac{4}{r}\right ),$$从而它们的中点 $E$ 的坐标为$$E\left(\sqrt{3}\left(\dfrac r4+\dfrac 1r\right ),\dfrac r4-\dfrac 1r\right).$$于是 $E$ 点的坐标 $(x,y)$ 满足$$\left(\dfrac{x}{\sqrt 3}\right)^2-y^2=1.$$其实上，当 $r$ 变成 $-r$ 时，$C$、$D$ 在第二、四象限，中点 $E$ 也满足上面的方程，从而点 $E$ 的轨迹的一部分为双曲线$$\dfrac{x^2}{3}-y^2=1.$$另外，当点 $C$、$D$ 分别在第一、二象限或第三、四象限时，点 $E$ 的轨迹为另一组双曲线：$$\dfrac{x^2}{3}-y^2=-1.$$如下图：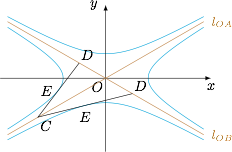
易知，“区域 $X$”为这两组双曲线所夹的“四角形”区域，除去原点．下面我们来判断四个命题的真假：
对于 ①，$I$ 可能在 $x$ 轴上，也可能在 $y$ 轴上，当 $I$ 在 $x$ 轴上时，圆上恰有一个点 $(\sqrt 3,0)$ 在区域 $X$ 内，① 错误；
对于 ②，当 $E$ 的轨迹为焦点在 $y$ 轴上的双曲线时，所以 $|OE|_{\min}=1$，② 错误；
对于 ③，因为 $S_1=\dfrac 12|ME|\cdot|NE|\sin 120^\circ$，$S_2=S_{\triangle GEF}=\dfrac 12|GE|\cdot|EF|\sin60^\circ$，所以有 $S_2>S_1$，③ 正确，如图：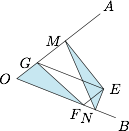
对于 ④，因为原点不在区域 $X$ 内，所以不存在这样的直线．
现在两条互相垂直的直线变成了夹角为 $60^\circ$ 的两条直线，我们猜测点 $E$ 的轨迹仍然为两条双曲线，下面给出严格推导：以 $l_{OA},l_{OB}$ 的两条角平分线为坐标轴建立直角坐标系，使得 $\angle xOA=\angle xOB=30^\circ $，先考虑点 $C$、$D$ 分别在第一、四象限时点 $E$ 的轨迹：
设 $|OC|=r$，则 $|OD|=\dfrac {4}{r}$，于是$$C\left(\dfrac{\sqrt 3}{2}r,\dfrac 12 r\right ),D\left(\dfrac{\sqrt 3}{2}\cdot \dfrac{4}{r},-\dfrac 12\cdot\dfrac{4}{r}\right ),$$从而它们的中点 $E$ 的坐标为$$E\left(\sqrt{3}\left(\dfrac r4+\dfrac 1r\right ),\dfrac r4-\dfrac 1r\right).$$于是 $E$ 点的坐标 $(x,y)$ 满足$$\left(\dfrac{x}{\sqrt 3}\right)^2-y^2=1.$$其实上，当 $r$ 变成 $-r$ 时，$C$、$D$ 在第二、四象限，中点 $E$ 也满足上面的方程，从而点 $E$ 的轨迹的一部分为双曲线$$\dfrac{x^2}{3}-y^2=1.$$另外，当点 $C$、$D$ 分别在第一、二象限或第三、四象限时，点 $E$ 的轨迹为另一组双曲线：$$\dfrac{x^2}{3}-y^2=-1.$$如下图：
易知，“区域 $X$”为这两组双曲线所夹的“四角形”区域，除去原点．下面我们来判断四个命题的真假：对于 ①，$I$ 可能在 $x$ 轴上，也可能在 $y$ 轴上，当 $I$ 在 $x$ 轴上时，圆上恰有一个点 $(\sqrt 3,0)$ 在区域 $X$ 内，① 错误；
对于 ②，当 $E$ 的轨迹为焦点在 $y$ 轴上的双曲线时，所以 $|OE|_{\min}=1$，② 错误；
对于 ③，因为 $S_1=\dfrac 12|ME|\cdot|NE|\sin 120^\circ$，$S_2=S_{\triangle GEF}=\dfrac 12|GE|\cdot|EF|\sin60^\circ$，所以有 $S_2>S_1$，③ 正确，如图：
对于 ④，因为原点不在区域 $X$ 内，所以不存在这样的直线．
题目
答案
解析
备注
