已知 $\triangle ABC$ 满足 $A=\dfrac{\pi}3$，$\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\cdot \overrightarrow{BC}=0$，点 $M$ 在 $\triangle ABC$ 外，且 $MB=2MC=2$，则 $MA$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$[1,3]$
【解析】
易知 $\triangle ABC$ 为正三角形，如图，设 $MA=x$，$AB=BC=CA=t$，那么由左右两图分别应用托勒密定理可得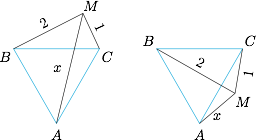
$$\begin{cases} tx\leqslant 3t,\\ 2t\leqslant tx+t,\end{cases}$$于是 $1\leqslant x\leqslant 3$．由于两侧等号均能取得（如下图），又根据图形连续变化，因此 $MA$ 的取值范围是 $[1,3]$．
$$\begin{cases} tx\leqslant 3t,\\ 2t\leqslant tx+t,\end{cases}$$于是 $1\leqslant x\leqslant 3$．由于两侧等号均能取得（如下图），又根据图形连续变化，因此 $MA$ 的取值范围是 $[1,3]$．
题目
答案
解析
备注
