已知点 $A(0,-1),B(3,0),C(1,2)$，平面区域 $P$ 是由所有满足 $\overrightarrow {AM}=\lambda\overrightarrow {AB}+\mu\overrightarrow {AC}$（其中 $2<\lambda <m,2<\mu<n$）的点 $M$ 组成的区域，若区域 $P$ 的面积为 $16$，则 $m+n$ 的最小值为 ．
【难度】
【出处】
无
【标注】
【答案】
$4+2\sqrt 2$
【解析】
向量 $\overrightarrow {AB}=(3,1)$，$\overrightarrow {AC}=(1,3)$，如图：
先考虑如何得到满足条件$$\overrightarrow {AM}=\lambda \overrightarrow {AB}+\mu\overrightarrow {AC}$$的点 $M$ 的位置（不考虑题目中 $\lambda,\mu$ 的范围）：
在直线 $AB,AC$ 上作出向量$$\overrightarrow {AM_1}=\lambda \overrightarrow {AB},\overrightarrow {AM_2}=\mu\overrightarrow {AC},$$过 $M_1,M_2$ 分别作 $AC,AB$ 的平行线，交于点 $M$，则$$\overrightarrow {AM}=\lambda \overrightarrow {AB}+\mu\overrightarrow {AC}.$$由此我们容易得到区域 $P$ 如下：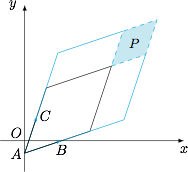
平行四边形的两边分别对应的向量为$$(m -2)\overrightarrow{AB},(n-2)\overrightarrow {AC},$$我们容易计算得以 $AB,AC$ 为邻边的平行四边形的面积为 $8$，所以区域 $P$ 的面积为 $8(m-2)(n-2)$，从而有$$(m-2)(n-2)=2.$$因为 $m>2,n>2$，由均值不等式知$$m-2+n-2\geqslant 2\sqrt{(m-2)(n-2)}=2\sqrt 2,$$从而有$$m+n\geqslant 4+2\sqrt 2,$$当且仅当 $m=n=2+\sqrt 2$ 时取到等号．
先考虑如何得到满足条件$$\overrightarrow {AM}=\lambda \overrightarrow {AB}+\mu\overrightarrow {AC}$$的点 $M$ 的位置（不考虑题目中 $\lambda,\mu$ 的范围）：在直线 $AB,AC$ 上作出向量$$\overrightarrow {AM_1}=\lambda \overrightarrow {AB},\overrightarrow {AM_2}=\mu\overrightarrow {AC},$$过 $M_1,M_2$ 分别作 $AC,AB$ 的平行线，交于点 $M$，则$$\overrightarrow {AM}=\lambda \overrightarrow {AB}+\mu\overrightarrow {AC}.$$由此我们容易得到区域 $P$ 如下：
平行四边形的两边分别对应的向量为$$(m -2)\overrightarrow{AB},(n-2)\overrightarrow {AC},$$我们容易计算得以 $AB,AC$ 为邻边的平行四边形的面积为 $8$，所以区域 $P$ 的面积为 $8(m-2)(n-2)$，从而有$$(m-2)(n-2)=2.$$因为 $m>2,n>2$，由均值不等式知$$m-2+n-2\geqslant 2\sqrt{(m-2)(n-2)}=2\sqrt 2,$$从而有$$m+n\geqslant 4+2\sqrt 2,$$当且仅当 $m=n=2+\sqrt 2$ 时取到等号．
题目
答案
解析
备注
