在四面体 $ABCD$ 中，已知 $AD\perp BC$，$AD=6$，且 $\dfrac{AB}{BD}=\dfrac{AC}{CD}=2$，则四面体 $ABCD$ 的体积的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$16$
【解析】
由于 $\dfrac{AB}{BD}=\dfrac{AC}{CD}=2$，于是 $B,C$ 在以 $EF$ 为直径的球 $O$ 的表面上，其中$$\overrightarrow{AE}=2\overrightarrow{ED},\overrightarrow{AF}=-2\overrightarrow{FD}.$$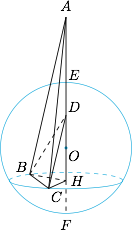
过 $BC$ 作与 $AD$ 垂直的平面得到圆 $H$，则 $H$ 必然在直线 $AD$ 上．此时四面体 $ABCD$ 的体积为$$\dfrac 13S_{\triangle BCH}\cdot AD= BH^2\cdot\sin \angle BHC\leqslant 16,$$等号当 $BH=4$ 且 $\angle BHC=90^\circ$ 时取得，也即 $H=O$，$\angle BOC$ 为直角时取得．因此四面体 $ABCD$ 的体积的最大值为 $16$．
过 $BC$ 作与 $AD$ 垂直的平面得到圆 $H$，则 $H$ 必然在直线 $AD$ 上．此时四面体 $ABCD$ 的体积为$$\dfrac 13S_{\triangle BCH}\cdot AD= BH^2\cdot\sin \angle BHC\leqslant 16,$$等号当 $BH=4$ 且 $\angle BHC=90^\circ$ 时取得，也即 $H=O$，$\angle BOC$ 为直角时取得．因此四面体 $ABCD$ 的体积的最大值为 $16$．
题目
答案
解析
备注
