若函数 $f(x)=x^2+\dfrac 2x-a\ln x$（$a>0$）存在唯一零点 $x_0$，且 $m<x_0<n$，其中 $m,n$ 为相邻的整数，则 $m+n=$ ．
【难度】
【出处】
无
【标注】
【答案】
$5$
【解析】
根据题意，方程$$x^2+\dfrac 2x-a\ln x=0$$有唯一解，也即函数 $g(x)=\dfrac{x^2+\dfrac 2x}{\ln x}$ 的图象与直线 $y=a$ 相切于 $(x_0,a)$．考虑到 $a>0$，因此只需要估计函数 $g(x)$ 的导函数在 $x>1$ 时的零点位置即可．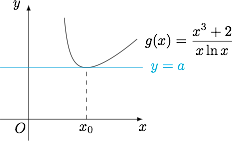
函数 $g(x)$ 的导函数$$g'(x)=\dfrac{(2x^3-2)\ln x-(x^3+2)}{x^2\ln^2x},$$设分子为 $\varphi(x)$，则$$\varphi(2)=14\ln 2-10<7\sqrt 2-10<0,$$而$$\varphi(3)=52\ln 3-29>0.$$其中用到了$$\ln 2<\sqrt 2-\dfrac{1}{\sqrt 2},$$这是因为对 $\ln x$ 的常用估计：$$\forall x>1,2\cdot\dfrac{x-1}{x+1}<\ln x<\sqrt x-\dfrac{1}{\sqrt x}.$$这样就得到了$$2<x_0<3,$$从而 $m+n$ 的值为 $5$．
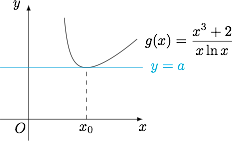函数 $g(x)$ 的导函数$$g'(x)=\dfrac{(2x^3-2)\ln x-(x^3+2)}{x^2\ln^2x},$$设分子为 $\varphi(x)$，则$$\varphi(2)=14\ln 2-10<7\sqrt 2-10<0,$$而$$\varphi(3)=52\ln 3-29>0.$$其中用到了$$\ln 2<\sqrt 2-\dfrac{1}{\sqrt 2},$$这是因为对 $\ln x$ 的常用估计：$$\forall x>1,2\cdot\dfrac{x-1}{x+1}<\ln x<\sqrt x-\dfrac{1}{\sqrt x}.$$这样就得到了$$2<x_0<3,$$从而 $m+n$ 的值为 $5$．
题目
答案
解析
备注
