如图，正三棱柱 $ABC-A'B'C'$ 的底面边长是 $1$，点 $D,E$ 分别是棱 $A'C',B'C'$ 的中点，四边形 $ADEB$ 的面积是 $\dfrac34$，则 $AA'=$ ．
【难度】
【出处】
2014年第二十五届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$\dfrac{\sqrt{13}}{4}$
【解析】
由题可知四边形 $ADEB$ 为等腰梯形，设其高为 $h$，则有$$S=\dfrac12\cdot(DE+AB)\cdot h,$$因此，可得 $h=1$，如图，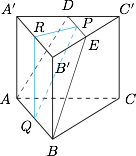
取 $DE,AB,A'B'$ 中点，记为 $P,Q,R$，则 $\triangle PQR$ 是以 $R$ 为顶点的直角三角形，且$$PQ=1 , PR=\dfrac12\cdot\dfrac{\sqrt3}{2}\cdot A'C'=\dfrac{\sqrt3}{4} QR=AA',$$因此，有 $AA'=\dfrac{\sqrt{13}}{4}$．
取 $DE,AB,A'B'$ 中点，记为 $P,Q,R$，则 $\triangle PQR$ 是以 $R$ 为顶点的直角三角形，且$$PQ=1 , PR=\dfrac12\cdot\dfrac{\sqrt3}{2}\cdot A'C'=\dfrac{\sqrt3}{4} QR=AA',$$因此，有 $AA'=\dfrac{\sqrt{13}}{4}$．
题目
答案
解析
备注
