在平面直角坐标系内，曲线 ${\log_x}y={\log_y}x$ 与抛物线 $y=x^2$ 的交点的个数是 ．
【难度】
【出处】
2014年第二十五届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$0$
【解析】
利用换底公式，曲线 ${\log_x}y={\log_y}x$ 化为$${\ln}x^2={\ln}y^2,$$根据对数函数的性质，即$$y=\begin{cases}x,&x>1,\\\dfrac1x,&0<x<1,\end{cases}$$与抛物线 $y=x^2$ 的图象如下．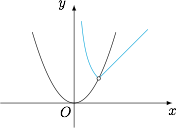
因此，交点个数为 $0$．
因此，交点个数为 $0$．
题目
答案
解析
备注
