$\triangle ABC$ 中，$BC$ 边上的中垂线分别交 $BC,AC$ 于 $D,M$．若 $\overrightarrow{AM}\cdot\overrightarrow{BC}=6$，$AB=2$，则 $AC=$ ．
【难度】
【出处】
无
【标注】
【答案】
$4$
【解析】
连接 $BM$，设 $\angle AMB=2\angle MCB=2\theta$，$MA=a$，$MB=b$．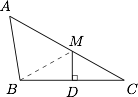
根据题意，有$$\overrightarrow{AM}\cdot \overrightarrow{BC}=2ab\cos^2\theta=6,$$从而 $ab\cos^2\theta=3$．在 $\triangle ABM$ 中，有$$4=a^2+b^2-2ab\cos 2\theta=a^2+b^2-2ab(2\cos^2\theta-1)=(a+b)^2-4ab\cos^2\theta,$$于是 $(a+b)^2=16$，从而 $AC=a+b=4$．
根据题意，有$$\overrightarrow{AM}\cdot \overrightarrow{BC}=2ab\cos^2\theta=6,$$从而 $ab\cos^2\theta=3$．在 $\triangle ABM$ 中，有$$4=a^2+b^2-2ab\cos 2\theta=a^2+b^2-2ab(2\cos^2\theta-1)=(a+b)^2-4ab\cos^2\theta,$$于是 $(a+b)^2=16$，从而 $AC=a+b=4$．
题目
答案
解析
备注
