设 $t$ 是正实数，双曲线 $x^2-y^2=t$ 的右焦点为 $F$，过 $F$ 任作一条直线交双曲线的右支于 $A,B$ 两点，设线段 $AB$ 的垂直平分线交 $x$ 轴于点 $P$，则 $\dfrac{|FP|}{|AB|}$ 的值为 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\sqrt 2}2$
【解析】
如图，不妨设直线 $AB$ 的倾斜角为锐角 $\theta$，且 $|AF|>|BF|$．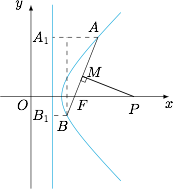
根据双曲线的第二定义，有$$\dfrac{|FP|}{|AB|}=\dfrac{|MF|}{|AB|\cos\theta}=\dfrac{|AF|-|BF|}{2(|AA_1|-|BB_1|)}=\dfrac{\sqrt 2}2.$$
根据双曲线的第二定义，有$$\dfrac{|FP|}{|AB|}=\dfrac{|MF|}{|AB|\cos\theta}=\dfrac{|AF|-|BF|}{2(|AA_1|-|BB_1|)}=\dfrac{\sqrt 2}2.$$
题目
答案
解析
备注
