记 $[x]$ 为不超过 $x$ 的最大整数，如 $[-0.2]=-1$，$[4.7]=4$．对于函数 $f(x)=\dfrac {[x]}{x}$，下列命题中真命题有 ．
① $f(x)$ 是周期为 $1$ 的函数；
② $\forall x \in \mathbb Z$，$f\left(x+\dfrac 12\right)+f\left(-x-\dfrac 12\right)=2$；
③ $f(x)$ 在每个形如 $(k,k+1)$，$k\in \mathbb N^*$ 的区间上均单调递减，在每个形如 $(-k,-k+1)$，$k\in \mathbb N^*$ 的区间上均单调递增；
④ $f(x)$ 的值域为 $[0,+\infty)$．
① $f(x)$ 是周期为 $1$ 的函数；
② $\forall x \in \mathbb Z$，$f\left(x+\dfrac 12\right)+f\left(-x-\dfrac 12\right)=2$；
③ $f(x)$ 在每个形如 $(k,k+1)$，$k\in \mathbb N^*$ 的区间上均单调递减，在每个形如 $(-k,-k+1)$，$k\in \mathbb N^*$ 的区间上均单调递增；
④ $f(x)$ 的值域为 $[0,+\infty)$．
【难度】
【出处】
无
【标注】
【答案】
②③
【解析】
① $f(x)$ 的定义域为 $(-\infty,0)\cup (0,+\infty) $，因此 $f(x)$ 不具有周期性，① 错误；
② 对于整数 $x$，$f\left(x+\dfrac 12\right)+f\left(-x-\dfrac 12\right)=\dfrac {\left[x+\dfrac 12\right]}{x+\dfrac 12}+\dfrac {\left[-x-\dfrac 12\right]}{-x-\dfrac 12}=\dfrac {x}{x+\dfrac 12}+\dfrac {-x-1}{-x-\dfrac 12}=2$，② 正确；
③ 在每个形如 $(k,k+1)$，$k\in \mathbb N^*$ 的区间上，$f(x)=\dfrac kx$，单调递减；
在每个形如 $(-k,-k+1)$，$k\in \mathbb N^*$ 的区间上，$f(x)=\dfrac {-k}{x}$，单调递增；于是 ③ 正确；
④ 在 ③ 的基础上，画出函数 $y=f(x)$ 的图象如下：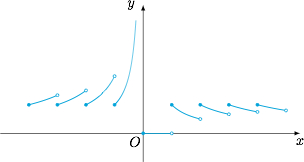
因此函数 $f(x)$ 的值域为 $\{0\}\cup \left(\dfrac 12,+\infty \right)$．
② 对于整数 $x$，$f\left(x+\dfrac 12\right)+f\left(-x-\dfrac 12\right)=\dfrac {\left[x+\dfrac 12\right]}{x+\dfrac 12}+\dfrac {\left[-x-\dfrac 12\right]}{-x-\dfrac 12}=\dfrac {x}{x+\dfrac 12}+\dfrac {-x-1}{-x-\dfrac 12}=2$，② 正确；
③ 在每个形如 $(k,k+1)$，$k\in \mathbb N^*$ 的区间上，$f(x)=\dfrac kx$，单调递减；
在每个形如 $(-k,-k+1)$，$k\in \mathbb N^*$ 的区间上，$f(x)=\dfrac {-k}{x}$，单调递增；于是 ③ 正确；
④ 在 ③ 的基础上，画出函数 $y=f(x)$ 的图象如下：
因此函数 $f(x)$ 的值域为 $\{0\}\cup \left(\dfrac 12,+\infty \right)$．
题目
答案
解析
备注
