函数 $f(x)$ 的导函数为 $f'(x)$，若对于定义域内任意 $x_1,x_2$（$x_1 \neq x_2$），有 $\dfrac {f(x_1)-f(x_2)}{x_1-x_2}=f'\left(\dfrac {x_1+x_2}{2}\right)$ 恒成立，则称 $f(x)$ 为恒均变函数．给出下列函数：
① $f(x)=2x+3$；② $f(x)=x^2-2x+3$；③ $f(x)=\dfrac 1x $；④ $f(x)={\mathrm e}^x$；⑤ $f(x)=\ln x$．
其中为恒均变函数的序号是 ．（写出所有满足条件的函数的序号）
① $f(x)=2x+3$；② $f(x)=x^2-2x+3$；③ $f(x)=\dfrac 1x $；④ $f(x)={\mathrm e}^x$；⑤ $f(x)=\ln x$．
其中为恒均变函数的序号是
【难度】
【出处】
无
【标注】
【答案】
①②
【解析】
“$\dfrac {f(x_1)-f(x_2)}{x_1-x_2}=f'\left(\dfrac {x_1+x_2}{2}\right)$”的两边都有很强的几何意义：
左边是指过点 $A(x_1,f(x_1))$，$B(x_2,f(x_2))$ 的割线斜率，
右边是指函数在 $AB$ 中点的横坐标处的切线斜率．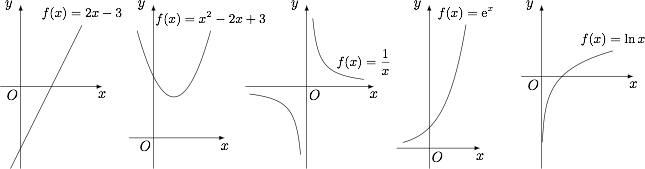
如图，很容易判断 ① 为恒均变函数．② 可能是恒均变函数，③④⑤ 应该不是恒均变函数．
对于 ②，尝试证明：$$\dfrac {f(x_1)-f(x_2)}{x_1-x_2}=\dfrac {(x_1+x_2)(x_1-x_2)-2(x_1-x_2)}{x_1-x_2}=x_1+x_2-2,$$$$f'\left(\dfrac {x_1+x_2}{2}\right)=2\cdot \dfrac {x_1+x_2}{2}-2=x_1+x_2-2.$$因此 ② 是恒均变函数．
对于 ③④⑤，尝试给出反例：
③：$$\dfrac {f(1)-f(3)}{1-3}=-\dfrac 13,f'(2)=-\dfrac 14;$$④：$$\dfrac {f(0)-f(2)}{0-2}=\dfrac {{\mathrm e}^2-1}{2},f'(1)={\mathrm e};$$⑤：$$\dfrac {f(1)-f(3)}{1-3}=\dfrac {\ln 3}{2},f'(2)=\dfrac 12.$$综上，填 ①②．
左边是指过点 $A(x_1,f(x_1))$，$B(x_2,f(x_2))$ 的割线斜率，
右边是指函数在 $AB$ 中点的横坐标处的切线斜率．
如图，很容易判断 ① 为恒均变函数．② 可能是恒均变函数，③④⑤ 应该不是恒均变函数．对于 ②，尝试证明：$$\dfrac {f(x_1)-f(x_2)}{x_1-x_2}=\dfrac {(x_1+x_2)(x_1-x_2)-2(x_1-x_2)}{x_1-x_2}=x_1+x_2-2,$$$$f'\left(\dfrac {x_1+x_2}{2}\right)=2\cdot \dfrac {x_1+x_2}{2}-2=x_1+x_2-2.$$因此 ② 是恒均变函数．
对于 ③④⑤，尝试给出反例：
③：$$\dfrac {f(1)-f(3)}{1-3}=-\dfrac 13,f'(2)=-\dfrac 14;$$④：$$\dfrac {f(0)-f(2)}{0-2}=\dfrac {{\mathrm e}^2-1}{2},f'(1)={\mathrm e};$$⑤：$$\dfrac {f(1)-f(3)}{1-3}=\dfrac {\ln 3}{2},f'(2)=\dfrac 12.$$综上，填 ①②．
题目
答案
解析
备注
