已知函数 $f\left(x\right) = \sin \dfrac{\mathrm \pi }{2}x$，任取 $t \in {\mathbb{R}}$，定义集合：$$A_t=\left\{y\mid y=f\left(x\right),\sqrt{(t-x)^2+(f(t)-f(x))^2}\leqslant \sqrt 2\right\}.$$设 ${M_t}$，${m_t}$ 分别表示集合 ${A_t}$ 中元素的最大值和最小值，记 $h\left(t\right) = {M_t} - {m_t}$．则
$(1)$ 函数 $h\left(t\right)$ 的最大值是 ；
$(2)$ 函数 $h\left(t\right)$ 的单调递增区间为 ．
$(1)$ 函数 $h\left(t\right)$ 的最大值是
$(2)$ 函数 $h\left(t\right)$ 的单调递增区间为
【难度】
【出处】
无
【标注】
【答案】
$(1)$ $2$；$(2)$ $(2k-1,2k), k\in \mathbb Z$
【解析】
考虑到周期性，取区间 $t\in [-2,2]$ 研究．
⑴ 如图，$h(t)$ 的最大值为 $h(0)=2$；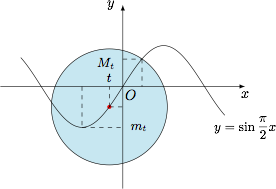
⑵ $h(-2)=2$，$h(-1)=1$，$h(0)=2$，$h(1)=1$，$h(2)=2$．
于是单调递增区间为 $(-1,0)$，$(1,2)$．
考虑到周期性，于是单调递增区间为 $(2k-1,2k), k\in \mathbb Z$．
⑴ 如图，$h(t)$ 的最大值为 $h(0)=2$；
⑵ $h(-2)=2$，$h(-1)=1$，$h(0)=2$，$h(1)=1$，$h(2)=2$．于是单调递增区间为 $(-1,0)$，$(1,2)$．
考虑到周期性，于是单调递增区间为 $(2k-1,2k), k\in \mathbb Z$．
题目
答案
解析
备注
