已知实数 $a>0$，$f(x)=\begin{cases}x^2-2ax,x \leqslant 1,\\ \log_{\frac 12}x,x>1.\end{cases}$ 若方程 $f(x)=-\dfrac 34a^2$ 有且仅有两个不等实根，且较大实根大于 $2$，则实数 $a$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac {2\sqrt 3}{3},2\right]$
【解析】
设 $x_1,x_2$（$x_1<x_2$）为两个不等实根，且由 $x_2>2$，得$$-\dfrac 34a^2= f(x_2)<-1,$$于是 $a>\dfrac {2\sqrt 3}{3}$．因此二次函数的对称轴在 $x=1$ 右侧，如图．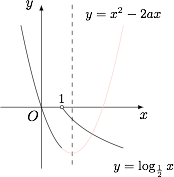
考虑到 $y=-\dfrac 34a^2$ 与函数图象的抛物线部分有交点，于是$$-\dfrac 34a^2\geqslant f(1)=1-2a,$$解得$$1\leqslant a \leqslant 2.$$综上，$a$ 的取值范围为 $\left(\dfrac {2\sqrt 3}{3},2\right]$．
考虑到 $y=-\dfrac 34a^2$ 与函数图象的抛物线部分有交点，于是$$-\dfrac 34a^2\geqslant f(1)=1-2a,$$解得$$1\leqslant a \leqslant 2.$$综上，$a$ 的取值范围为 $\left(\dfrac {2\sqrt 3}{3},2\right]$．
题目
答案
解析
备注
