对于实数 $ a $ 和 $ b $，定义运算" $ * $ "：$ a*b= \begin{cases} a^2-ab,a\leqslant b,\\b^2-ab,a>b.\end{cases} $ 设 $ f\left(x\right)=\left(2x-1\right)*\left(x-1\right) $，且关于 $ x $ 的方程 $ f\left(x\right)=m\left(m\in {\mathbb {R}}\right) $ 恰有三个互不相等的实数根 $ x_1$，$x_2$，$x_3 $，则 $ x_1x_2x_3 $ 的取值范围是 ．
【难度】
【出处】
2012年高考福建卷（理）
【标注】
【答案】
$ \left({\dfrac{1-{\sqrt{3}}}{16}},0 \right)$
【解析】
由已知条件可得 $ f\left(x\right)=\left(2x-1\right)*\left(x-1\right)= \begin{cases} 2x^2-x,x\leqslant 0,
\\ -x^2+x, x>0,\end{cases} $
该函数的图象如图所示，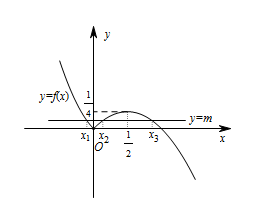
求得 $f(\dfrac {1-\sqrt 3}4)=f(\dfrac 12)=\dfrac 14$．
当 $0<m<\dfrac 14$ 时，方程 $ f\left(x\right)=m $ 有三个不同的实数根，
不妨设 $ x_1<x_2<x_3,$ 则 $ {\dfrac{1-{\sqrt{3}}}{4}}<x_1<0<x_2<{\dfrac{1}{2}}<x_3<1, $ 且 $ x_2+x_3=1, $
根据均值不等式，得 ${x_2}{x_3} < {\left( {\dfrac{{{x_2} + {x_3}}}{2}} \right)^2} = \dfrac{1}{4}$，
所以 $ 0>x_1x_2x_3>{\dfrac{1}{4}}x_1>{\dfrac{1}{4}}\times {\dfrac{1-{\sqrt{3}}}{4}}={\dfrac{1-{\sqrt{3}}}{16}} $，
当 $m$ 趋近于 $0$ 时，$x_1x_2x_3$ 趋近于 $0$，当 $m$ 趋近于 $\dfrac 14$ 时，$x_1x_2x_3$ 趋近于 $\dfrac {1-\sqrt 3}{16}$，
于是 $x_1x_2x_3$ 的取值范围为 $ \left({\dfrac{1-{\sqrt{3}}}{16}},0\right) $．
\\ -x^2+x, x>0,\end{cases} $
该函数的图象如图所示，
求得 $f(\dfrac {1-\sqrt 3}4)=f(\dfrac 12)=\dfrac 14$．当 $0<m<\dfrac 14$ 时，方程 $ f\left(x\right)=m $ 有三个不同的实数根，
不妨设 $ x_1<x_2<x_3,$ 则 $ {\dfrac{1-{\sqrt{3}}}{4}}<x_1<0<x_2<{\dfrac{1}{2}}<x_3<1, $ 且 $ x_2+x_3=1, $
根据均值不等式，得 ${x_2}{x_3} < {\left( {\dfrac{{{x_2} + {x_3}}}{2}} \right)^2} = \dfrac{1}{4}$，
所以 $ 0>x_1x_2x_3>{\dfrac{1}{4}}x_1>{\dfrac{1}{4}}\times {\dfrac{1-{\sqrt{3}}}{4}}={\dfrac{1-{\sqrt{3}}}{16}} $，
当 $m$ 趋近于 $0$ 时，$x_1x_2x_3$ 趋近于 $0$，当 $m$ 趋近于 $\dfrac 14$ 时，$x_1x_2x_3$ 趋近于 $\dfrac {1-\sqrt 3}{16}$，
于是 $x_1x_2x_3$ 的取值范围为 $ \left({\dfrac{1-{\sqrt{3}}}{16}},0\right) $．
题目
答案
解析
备注
