如图,点 $ D $ 在 $ \odot O $ 的弦 $ AB $ 上移动,$ AB=4 $,连接 $ OD $,过点 $ D $ 作 $ OD $ 的垂线交 $ \odot O $ 于点 $ C $,则 $ CD $ 的最大值为 .

【难度】
【出处】
2012年高考湖北卷(理)
【标注】
【答案】
$ 2 $
【解析】
连接 $ OC $,因为 $ CD={\sqrt{{OC}^2-{OD}^2}} $,且 $ OC $ 为 $ \odot O $ 的半径,是定值,
所以当 $ OD $ 取最小值时,$ CD $ 取最大值.
显然当 $ OD\perp AB $ 时,$ OD $ 取最小值,此时 $ CD={\dfrac{1}{2}}AB=2 $.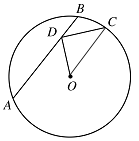
所以当 $ OD $ 取最小值时,$ CD $ 取最大值.
显然当 $ OD\perp AB $ 时,$ OD $ 取最小值,此时 $ CD={\dfrac{1}{2}}AB=2 $.

题目
答案
解析
备注