如图，在正三角形 $ABC$ 中，$D,E,F$ 分别是各边的中点，$G,H,I,J$ 分别是 $AF,AD,BE,DE$ 的中点，将 $\triangle ABC$ 沿 $DE,EF,FD$ 折成三棱锥后，$GH$ 与 $IJ$ 所在直线所成的角的大小为 ．
【难度】
【出处】
无
【标注】
【答案】
$60^\circ$
【解析】
如图．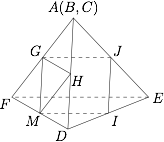
取 $DF$ 的中点，连接图中线段，则 $\angle HGM$ 为所求，显然 $\triangle GHM$ 为等边三角形，于是答案为 $60^\circ$．
取 $DF$ 的中点，连接图中线段，则 $\angle HGM$ 为所求，显然 $\triangle GHM$ 为等边三角形，于是答案为 $60^\circ$．
题目
答案
解析
备注
