查看数据源：599fd4de3020170007bcf972
函数 $f(x)=\sqrt{2x^2-2x+1}-\sqrt{2x^2+2x+5}$ 的值域是 ．
【难度】
【出处】
2017年中国科学技术大学综合评价测试数学试题（回忆版）
【标注】
  • 方法
    >
    数形结合
    >
    转化为距离
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的最值和值域
  • 知识点
    >
    代数变形
    >
    代数式的形
    >
    整形
    >
    根式的整理
【答案】
$\left[-2,\sqrt 2\right)$
【解析】
根据题意，有\[f(x)=\sqrt 2\cdot \left[\sqrt{\left(x-\dfrac 12\right)^2+\dfrac 14}-\sqrt{\left(x+\dfrac 12\right)^2+\dfrac 94}\right],\]设 $A\left(\dfrac 12,\dfrac 12\right)$，$B\left(-\dfrac 12,\dfrac 32\right)$，则 $f(x)$ 的几何意义是 $x$ 轴上的点 $P(x,0)$ 到点 $A$ 与到点 $B$ 的距离之差的 $\sqrt 2$ 倍，如图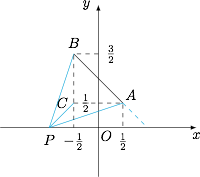．因此可得当 $P$ 位于线段 $BA$ 的延长线上时，$f(x)$ 取得最小值 $-\sqrt 2AB=-2$；当 $P$ 趋于 $x$ 轴负无穷远处时，$f(x)$ 趋于上确界 $AC=1$，其中 $C\left(-\dfrac 12,\dfrac 12\right)$．从而所求的值域为 $\left[-2,\sqrt 2\right)$．
题目 答案 解析 备注
0.111406s