三棱柱 $ ABC -A_1B_1C_1 $ 中,底面边长和侧棱长都相等,$ \angle BAA_1=\angle CAA_1=60^\circ $,则异面直线 $ AB_1 $ 与 $ BC_1 $ 所成角的余弦值为 .
【难度】
【出处】
2012年高考大纲全国卷(理)
【标注】
【答案】
$ {\dfrac{{\sqrt{6}}}{6}} $
【解析】
过点 $ A_1 $ 作 $ A_1O\perp 平面ABC $ 于点 $ O $,设 $ AB=a $,取 $ BC $ 的中点 $ D $,连接 $ AD $.
依题意,得 $ O $ 在 $ \angle BAC $ 的平分线 $ AD $ 上.
又 $ \triangle ABC $ 是正三角形,因此 $ AD\perp BC$,从而 $AA_1\perp BC$.
因为 $AA_1\parallel BB_1 $,所以 $BB_1\perp BC $,从而四边形 $ BCC_1B_1 $ 是正方形,$ BC_1={\sqrt{2}}a $.
过点 $ B_1 $ 作 $ B_1E\parallel BC_1 $ 交 $ CB $ 的延长线于点 $ E $,连接 $ AE $,
则 $ \angle AB_1E $(或其补角)是异面直线 $ AB_1 $ 与 $ BC_1 $ 所成的角.
在 $ \triangle AB_1E $ 中,$ AB_1={\sqrt{3}}a $,$ B_1E=BC_1={\sqrt{2}}a $,\[ AE= {\sqrt{a^2+ a^2-2\times a\times a\cos 120^\circ }}={\sqrt{3}}a, \]\[ \cos \angle AB_1E={\dfrac{{B_1A}^2+{B_1E}^2-{AE}^2}{2B_1A\cdot B_1E}}={\dfrac{{\sqrt{6}}}{6}}, \]因此异面直线 $ AB_1 $ 与 $ BC_1 $ 所成角的余弦值是 $ {\dfrac{{\sqrt{6}}}{6}} $.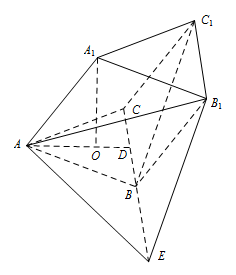
依题意,得 $ O $ 在 $ \angle BAC $ 的平分线 $ AD $ 上.
又 $ \triangle ABC $ 是正三角形,因此 $ AD\perp BC$,从而 $AA_1\perp BC$.
因为 $AA_1\parallel BB_1 $,所以 $BB_1\perp BC $,从而四边形 $ BCC_1B_1 $ 是正方形,$ BC_1={\sqrt{2}}a $.
过点 $ B_1 $ 作 $ B_1E\parallel BC_1 $ 交 $ CB $ 的延长线于点 $ E $,连接 $ AE $,
则 $ \angle AB_1E $(或其补角)是异面直线 $ AB_1 $ 与 $ BC_1 $ 所成的角.
在 $ \triangle AB_1E $ 中,$ AB_1={\sqrt{3}}a $,$ B_1E=BC_1={\sqrt{2}}a $,\[ AE= {\sqrt{a^2+ a^2-2\times a\times a\cos 120^\circ }}={\sqrt{3}}a, \]\[ \cos \angle AB_1E={\dfrac{{B_1A}^2+{B_1E}^2-{AE}^2}{2B_1A\cdot B_1E}}={\dfrac{{\sqrt{6}}}{6}}, \]因此异面直线 $ AB_1 $ 与 $ BC_1 $ 所成角的余弦值是 $ {\dfrac{{\sqrt{6}}}{6}} $.

题目
答案
解析
备注