设 $f(x)=\dfrac{|x|}{x+3}$，若关于 $x$ 的方程 $f(x)=kx^2$ 有四个不同的实数解，则实数 $k$ 的取值范围是 ．
【难度】
【出处】
2016年第二十七届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$\left(\dfrac94,+\infty\right)$
【解析】
注意到 $x=0$ 是方程 $f(x)=kx^2$ 的一个解，且 $k=0$ 时，方程仅有一个解，因此题意即$$\dfrac1k=\dfrac{|x|}{x}\cdot x(x+3),$$在 $x\ne0$ 时，有三个不同的实数解，令 $g(x)=\dfrac{|x|}{x}\cdot x(x+3)$，其图象如下．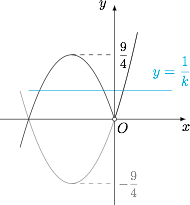
于是直线 $y=\dfrac1k$ 与 $y=g(x)$ 的图象公共点个数 $n$ 对应关系为\[\begin{array}
{c|cccc} \hline
\dfrac1k&(-\infty,0]&\left(0,\dfrac49\right)&\dfrac49&\left(\dfrac49,+\infty\right)\\ \hline
n&1&3&2&1 \\ \hline
\end{array}\]再结合 $x=0$ 为一个实数解，故实数 $k$ 的取值范围为 $\left(\dfrac94,+\infty\right)$．
于是直线 $y=\dfrac1k$ 与 $y=g(x)$ 的图象公共点个数 $n$ 对应关系为\[\begin{array}{c|cccc} \hline
\dfrac1k&(-\infty,0]&\left(0,\dfrac49\right)&\dfrac49&\left(\dfrac49,+\infty\right)\\ \hline
n&1&3&2&1 \\ \hline
\end{array}\]再结合 $x=0$ 为一个实数解，故实数 $k$ 的取值范围为 $\left(\dfrac94,+\infty\right)$．
题目
答案
解析
备注
