已知 $a_1,a_2,\cdots ,a_{2016}\in [-2,2]$，$a_1+a_2+\cdots +a_{2016}=0$，则 $a_1^3+a_2^3+\cdots +a_{2016}^3$ 的最大值为 ．
【难度】
【出处】
无
【标注】
【答案】
$4032$
【解析】
取 $f(x)=x^3$ 过点 $(2,8)$ 的切线 $y=3x+2$，则$$x^3\leqslant 3x+2,$$等号当且仅当 $x=-1$ 或 $x=2$ 时取得，如图：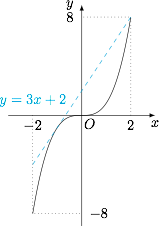
因此$$a_1^3+a_2^3+\cdots +a_{2016}^3\leqslant 3(a_1+a_2+\cdots +a_{2016})+4032=4032,$$等号当 $a_1,a_2,\cdots ,a_{2016}$ 中有 $672$ 个数取 $2$，其余的数取 $-1$ 时取得．
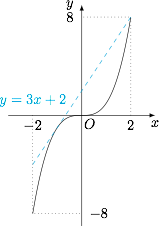因此$$a_1^3+a_2^3+\cdots +a_{2016}^3\leqslant 3(a_1+a_2+\cdots +a_{2016})+4032=4032,$$等号当 $a_1,a_2,\cdots ,a_{2016}$ 中有 $672$ 个数取 $2$，其余的数取 $-1$ 时取得．
题目
答案
解析
备注
