已知 $M(3,2)$，点 $P$ 在 $y$ 轴上运动，点 $Q$ 在圆 $C:(x-1)^2+(y+2)^2=4$ 上运动，则 $\overrightarrow {MP}+\overrightarrow {MQ}$ 的长度的最小值是 ．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
此问题中 $P,Q$ 都是动点，考虑先固定其中的一个动点，让另一个动点移动，看看何时 $\overrightarrow {MP}+\overrightarrow {MQ}$ 的长度取到最值．
考虑后发现先固定点 $Q$ 比较容易（先固定点 $P$ 则需要根据 $P$ 点的位置不同进行讨论），如图：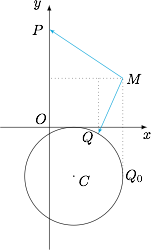
当点 $Q$ 固定时，考虑 $\overrightarrow {MP}+\overrightarrow {MQ}$ 的坐标：
点 $P$ 的移动不改变这个和向量的横坐标，所以当这个和向量的纵坐标为零时，对应的长度有最小值，且纵坐标一定可以取到零．
接下来让点 $Q$ 在圆上移动，考虑和向量的横坐标的绝对值何时最小：
因为 $\overrightarrow {MP}$ 的横坐标恒为 $-3$，$\overrightarrow {MQ}$ 的横坐标小于等于零，所以当 $\overrightarrow {MQ}$ 的横坐标为零时，和向量横坐标的绝对值最小，此时 $\overrightarrow {MP}+\overrightarrow {MQ}$ 的长度有最小值 $3$．容易求出此时 $Q(3,-2),P(0,6)$．
考虑后发现先固定点 $Q$ 比较容易（先固定点 $P$ 则需要根据 $P$ 点的位置不同进行讨论），如图：
当点 $Q$ 固定时，考虑 $\overrightarrow {MP}+\overrightarrow {MQ}$ 的坐标：点 $P$ 的移动不改变这个和向量的横坐标，所以当这个和向量的纵坐标为零时，对应的长度有最小值，且纵坐标一定可以取到零．
接下来让点 $Q$ 在圆上移动，考虑和向量的横坐标的绝对值何时最小：
因为 $\overrightarrow {MP}$ 的横坐标恒为 $-3$，$\overrightarrow {MQ}$ 的横坐标小于等于零，所以当 $\overrightarrow {MQ}$ 的横坐标为零时，和向量横坐标的绝对值最小，此时 $\overrightarrow {MP}+\overrightarrow {MQ}$ 的长度有最小值 $3$．容易求出此时 $Q(3,-2),P(0,6)$．
题目
答案
解析
备注
