已知空间四边形 $ABCD$ 的四个顶点都在球 $O$ 的球面上，$E,F$ 分别是 $AB,CD$ 的中点，且 $EF\perp AB$，$EF\perp CD$．若 $AB=EF=4$，$CD=8$，则球 $O$ 的半径为 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac{\sqrt{65}}2$
【解析】
如图，线段 $AB$ 和 $CD$ 分别是圆台两个底面的直径，$EF$ 是连接底面中心的线段．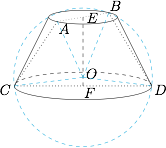
根据题意，球 $O$ 的半径 $r$ 满足\[r^2=OE^2+\left(\dfrac 12AB\right)^2=OF^2+\left(\dfrac 12CD\right)^2,\]于是\[OE^2-OF^2=\left(\dfrac 12CD\right)^2-\left(\dfrac 12AB\right)^2=12,\]因此 $O$ 在线段 $EF$ 上，$$OE+OF=4,OE-OF=3,$$于是 $OF=\dfrac 12$，进而所求半径\[r=\sqrt{OF^2+\left(\dfrac 12CD\right)^2}=\dfrac{\sqrt{65}}2.\]
根据题意，球 $O$ 的半径 $r$ 满足\[r^2=OE^2+\left(\dfrac 12AB\right)^2=OF^2+\left(\dfrac 12CD\right)^2,\]于是\[OE^2-OF^2=\left(\dfrac 12CD\right)^2-\left(\dfrac 12AB\right)^2=12,\]因此 $O$ 在线段 $EF$ 上，$$OE+OF=4,OE-OF=3,$$于是 $OF=\dfrac 12$，进而所求半径\[r=\sqrt{OF^2+\left(\dfrac 12CD\right)^2}=\dfrac{\sqrt{65}}2.\]
题目
答案
解析
备注
