已知 $f(x)=x+\dfrac2x$,则函数 $y=f\left(f(x)\right)$ 的单调递增区间是 .
【难度】
【出处】
2013年第二十四届“希望杯”全国数学邀请赛高二(二试)
【标注】
【答案】
$\left(-\infty,-\sqrt2\right)$ 和 $\left(\sqrt2,+\infty\right)$
【解析】
依据对勾函数的性质,函数 $f(x)$ 的值域为 $\left(-\infty,-2\sqrt2\right)\cup\left(2\sqrt2,+\infty\right)$,且单调递减区间为 $\left(-\sqrt2,0\right)$ 和 $\left(0,\sqrt2\right)$,单调递增区间为 $\left(-\infty,-\sqrt2\right)$ 和 $\left(\sqrt2,+\infty\right)$,再结合复合函数的单调性,可知函数 $y=f\left(f(x)\right)$ 的单调递增区间为 $\left(-\infty,-\sqrt2\right)$ 和 $\left(\sqrt2,+\infty\right)$.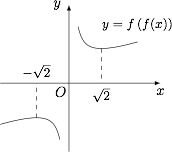

题目
答案
解析
备注