将边长为 $1$ 的正方形 $ABCD$ 沿对角线 $AC$ 折起，使 $D$ 点变到 $D'$ 点，得到三棱锥 $D'-ABC$．若 $D'A=D'B$，则三棱锥 $D'-ABC$ 的体积是 ，侧面 $ABD'$ 与 $BCD'$ 的夹角的余弦值是 ．
【难度】
【出处】
2013年第二十四届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$\dfrac{\sqrt2}{12}$；$-\dfrac13$
【解析】
如图，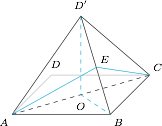
连接 $AC$，取 $AC$ 中点记为 $O$，则$$D'O=BO=\dfrac{\sqrt2}{2}.$$结合 $D'A=D'B=1$，由勾股定理可知 $\triangle D'OB$ 是直角三角形，由此 $D'O\perp ABCD$，故三棱锥 $D'-ABC$ 的体积是$$V_{D'-ABC}=\dfrac13\cdot S_{\triangle ABC}\cdot D'O=\dfrac{\sqrt2}{12}.$$注意到 $AC\perp D'OB$，$\triangle D'AB,\triangle D'CB$ 均是等边三角形，取 $D'B$ 的中点记为 $E$，连接 $AE,CE$，则 $\angle AEC$ 即为两侧面的夹角，利用余弦定理可得$$\cos\angle AEC=\dfrac{AE^2+EC^2-AC^2}{2\cdot AE\cdot EC}=-\dfrac13,$$因此两侧面的夹角的余弦值为 $-\dfrac13$．
连接 $AC$，取 $AC$ 中点记为 $O$，则$$D'O=BO=\dfrac{\sqrt2}{2}.$$结合 $D'A=D'B=1$，由勾股定理可知 $\triangle D'OB$ 是直角三角形，由此 $D'O\perp ABCD$，故三棱锥 $D'-ABC$ 的体积是$$V_{D'-ABC}=\dfrac13\cdot S_{\triangle ABC}\cdot D'O=\dfrac{\sqrt2}{12}.$$注意到 $AC\perp D'OB$，$\triangle D'AB,\triangle D'CB$ 均是等边三角形，取 $D'B$ 的中点记为 $E$，连接 $AE,CE$，则 $\angle AEC$ 即为两侧面的夹角，利用余弦定理可得$$\cos\angle AEC=\dfrac{AE^2+EC^2-AC^2}{2\cdot AE\cdot EC}=-\dfrac13,$$因此两侧面的夹角的余弦值为 $-\dfrac13$．
题目
答案
解析
备注
