双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$（$a,b>0$）的左右焦点分别是 $F_1,F_2$，过 $F_2$ 的直线交双曲线的右支于点 $M$ 和 $N$．又点 $A,B$ 分别是 $\triangle MF_1F_2,\triangle NF_1F_2$ 的内心．当离心率 $e=2$，$|AB|=\dfrac92$，直线 $MN$ 倾斜角的正弦值为 $\dfrac89$ 时，$a=$ ，双曲线的方程是 ．
【难度】
【出处】
2013年第二十四届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$2$；$\dfrac{x^2}{4}-\dfrac{y^2}{12}=1$
【解析】
设双曲线与 $x$ 轴正半轴的交点即为 $H(a,0)$，根据双曲线内心的性质，可知点 $A,B$ 的横坐标均为 $a$，连接 $AF_2,BF_2$，如图．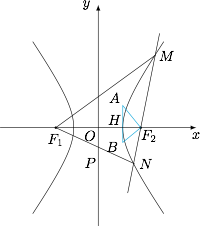
设 $\angle AF_2H=\alpha,\angle BF_2H=\beta$，根据三角形内心为角平分线交点，可知$$\alpha+\beta=\dfrac{\pi}{2},\sin2\alpha=\dfrac89,$$根据 $|AB|=\dfrac92$，结合离心率为 $2$，有$$|AB|=|AH|+|BH|=(c-a)\cdot\left(\tan\alpha+\dfrac{1}{\tan\alpha}\right)=a\cdot\left(\tan\alpha+\dfrac{1}{\tan\alpha}\right)=\dfrac{2a}{\sin2\alpha}=\dfrac92,$$解得 $a$ 的值为 $2$，双曲线的方程为 $\dfrac{x^2}{4}-\dfrac{y^2}{12}=1$．
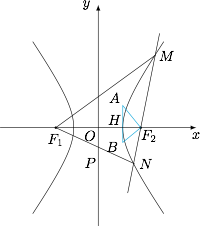设 $\angle AF_2H=\alpha,\angle BF_2H=\beta$，根据三角形内心为角平分线交点，可知$$\alpha+\beta=\dfrac{\pi}{2},\sin2\alpha=\dfrac89,$$根据 $|AB|=\dfrac92$，结合离心率为 $2$，有$$|AB|=|AH|+|BH|=(c-a)\cdot\left(\tan\alpha+\dfrac{1}{\tan\alpha}\right)=a\cdot\left(\tan\alpha+\dfrac{1}{\tan\alpha}\right)=\dfrac{2a}{\sin2\alpha}=\dfrac92,$$解得 $a$ 的值为 $2$，双曲线的方程为 $\dfrac{x^2}{4}-\dfrac{y^2}{12}=1$．
题目
答案
解析
备注
