已知矩形 $ABCD$ 中，$AB=2$，$AD=1$，$E$ 点在 $AB$ 上，$AE=a$（$0<a<1$）．小明从 $E$ 点出发在矩形内行进，依次经过矩形三边 $AD,DC,CB$ 上的一点（不含顶点）后，回到 $E$ 点，则小明行进的路程最短是 ．
【难度】
【出处】
2013年第二十四届“希望杯”全国数学邀请赛高二（一试）
【标注】
【答案】
$2\sqrt5$
【解析】
根据对称性可知，题意相当于小明依次经过线段 $AD,DC',C'B'$（不包括端点）到达点 $E'$，如图．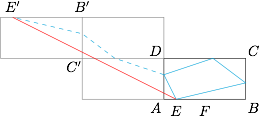
因此，小明走过的最短距离是线段 $EE'$ 的长度为 $2\sqrt5$．
因此，小明走过的最短距离是线段 $EE'$ 的长度为 $2\sqrt5$．
题目
答案
解析
备注
