某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的长方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=新工件的体积/原工件的体积） \((\qquad)\) 
【难度】
【出处】
2015年高考湖南卷（理）
【标注】
【答案】
A
【解析】
为了能够从圆锥形的工料中加工出长方体形的工件，需要首先将圆锥加工成一个圆柱，然后从圆柱中加工成长方体，如图．
因此，我们可以分两步计算工料的材料利用率，如图．
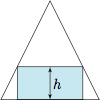设圆柱的高为 $h$，则第一步的材料利用率为$$\dfrac{\pi\left(1-\dfrac 12h\right)^2\cdot h}{\dfrac 23\pi}\leqslant \dfrac 49,$$等号当且仅当 $1-\dfrac 12h=h$，即 $h=\dfrac 23$ 时取得（这里用到了三元的均值不等式）．
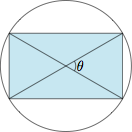另一方面，我们熟知第二步的材料利用率最高为 $\dfrac 2\pi$．
综上，工料的材料利用率最高为$$\dfrac 49\times\dfrac 2\pi=\dfrac{8}{9\pi}.$$
因此，我们可以分两步计算工料的材料利用率，如图．设圆柱的高为 $h$，则第一步的材料利用率为$$\dfrac{\pi\left(1-\dfrac 12h\right)^2\cdot h}{\dfrac 23\pi}\leqslant \dfrac 49,$$等号当且仅当 $1-\dfrac 12h=h$，即 $h=\dfrac 23$ 时取得（这里用到了三元的均值不等式）．另一方面，我们熟知第二步的材料利用率最高为 $\dfrac 2\pi$．综上，工料的材料利用率最高为$$\dfrac 49\times\dfrac 2\pi=\dfrac{8}{9\pi}.$$
题目
答案
解析
备注
